An object is dropped from an altitude of one Earth radius above Earth’s surface. If M is the mass of Earth and R is its radius. The speed of the object just before it hits Earth is given by:

A

$\sqrt{G M / R}$

B

$\sqrt{G M / 2 R}$

C

$\sqrt{2 G M / R}$

D

$\sqrt{G M / R^{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Gain in K.E. = Loss in G.P.E. $\Rightarrow \frac{1}{2} m v^{2} = - \frac{G m M}{2 R} - (\frac{- G m M}{R}) = \frac{G m M}{2 R} \Rightarrow v = \sqrt{\frac{G M}{R}}$

|

Updated on:21/07/2023

Class 12 PHYSICS GRAVITATION

Similar Questions

Knowledge Check

Question 1 - Select One
A satellite of mass m is orbiting the earth at a height h from its surface. If M is the mass of the earth and R its radius, the kinetic energy of the stellite will be
A $- \frac{G m M}{{(R + h)}^{2}}$
B $\frac{G m M}{2 {(R + h)}^{2}}$
C $\frac{G m M}{(R + h)}$
D $\frac{G m M}{2 (R + h)}$
Question 2 - Select One
A body is dropped from a height $R_{e}$ (radius of earth) above the earth's surface. It strikes the earth with speed $v_{0}$ , if $v_{e}$ is the escape velocity from earth’s surface, then $\frac{v_{0}}{v_{e}}$ is
A $\sqrt{2} : 1$
B $1 : 2$
C $1 : \sqrt{2}$
D $2 : 1$
Question 3 - Select One
A geostationary satellite is at a height $h$ above the surface of earth. If earth radius is $R$ -

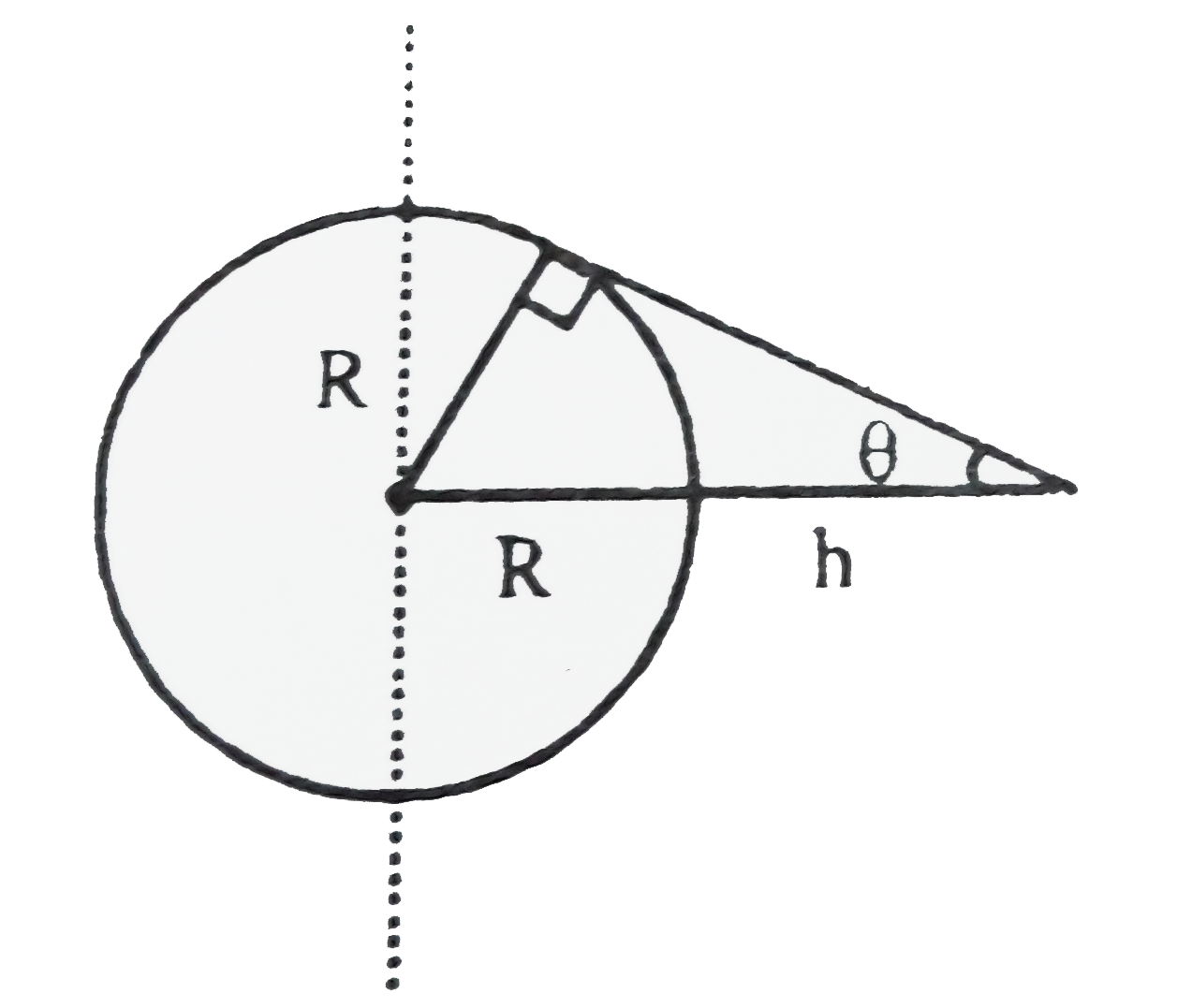AThe minimum colatitude on earth upto which the satellite can be used for communication is ${sin}^{- 1} (R / R + h)$
BThe maximum colatitudes on earth upto which the satellite can be used for communication is ${sin}^{- 1} (R / R + h)$
CThe area on earth escaped from this satellite is given as $(2 π R^{2} (1 + sin θ))$
DThe area on earth escaped from this satellite is given as $(2 π R^{2} (1 + cos θ)$

Recommended Questions

Home
Ask Doubt
Profile