Three planets of same density and with radii R1,R2 and R3 such that R1=2R2=3R3 have gravitation fields strength on planets are v1,v2,v3, respectively. Then :
g1/g2=1/2
g1/g3=3
v1/v2=2
v1/v3=1/3
The correct Answer is:B, C, D
v=√2qR=√2GMR=√2GR(ρ43πR3)=√8πGP3R
Therefore , ⇒v1v2=R1R2=2,g1g2=3,g1g3=R1R3=3,v1v3=R1R3=3
g=GMR2=GR2(ρ43πR3)=5πGP3R
Similar Questions
Three planets of same density have radii R1,R2 and R3 such that R1=2R2=3R3. The gravitational field at their respective surfaces are g1,g2 and g3 and escape velocities from their surfeces are υ1,υ2 and υ3, then
View SolutionTwo planets A and B have the same average density . Their radii RAandRB are such that RA:RB=3:1 . If gAandgB are the acceleration due to gravity at the surface of the planets , the gA:gB equals
View Solution
Knowledge Check
Three planets of same density have radii R1,R2 and R3 such that R1=2R2=3R3. The gravitational field at their respective surfaces are g1,g2 and g3 and escape velocities from their surfeces are υ1,υ2 and υ3, then
Ag1/g2=2Bg1/g3=3Cυ1/υ2=1/4Dυ1/υ3=3Two planets have the same average density but their radii are R1 and R2. If acceleration due to gravity on these planets be g1 and g2 respectively, then
Ag1g2=R1R2Bg1g2=R2R1Cg1g2=R21R22Dg1g2=R31R32In an electric circuit three resistors R1,R2andR3 are connected in series such that R2=R3. IF V1,V2andV3 are the voltage across R1,R2andR3 respectively , then
AV1=V2BV2=V3CV1=V3DV1=V2=V3
Two planets A and B have the same averge density . Their radii RAandRB are such that RA:RB=3:1. If gA and gB are the acceleration due to gravity at the surfaces of the planets, the gA:gB equals
View SolutionFigure shows three resistor configurations R1,R2andR3 connected to 3V battery. If the power dissipated by the configuration R1,R2andR3 is P1,P2andP3, respectively. Then -
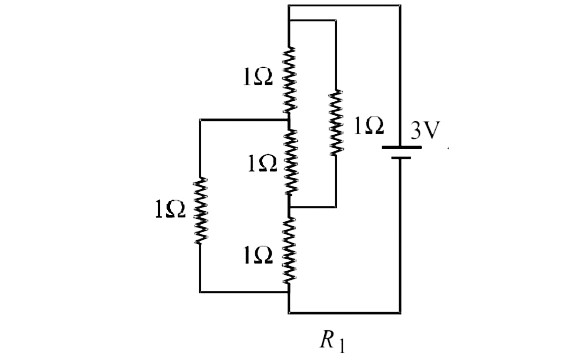
View SolutionFigure shows three resistor configurations R1,R2 and R3 connected to 3 V battery .

If the powers dissipated by the configuration R1,R2 and R3 are P1,P2 and P3, respectively, then
View SolutionSuppose there are two planets, 1 and 2, having the same density but their radii are R1andR2 respectively, where R1>R2. The accelerations due to gravity on the surface of these planets are related as
View SolutionTwo planets A and B have the same averge density . Their radii RAandRB are such that RA:RB=3:1. If gA and gB are the acceleration due to gravity at the surfaces of the planets, the gA:gB equals
View Solution
