Two adiabatic expansions of n mole of same gas are shown. If VBVA=VDVC×12 then TC/TD is :

20.4TATB
21.4TATB
TATB12(0.4)
TATB
The correct Answer is:A
TAVγ−1A=TBVγ−1B⇒TA/TB=(VBVA)γ−1
and TCVγ−1C=TDVγ−1D⇒TC/TD=(VDVC)γ−1⇒TCTD=(2VBVA)γ−1=2γ−1TATB⇒ΔT=(165−1)1RK=115RKΔQ=ΔU+W, Here, Q : U and W all different forms of energy.For isothermal process, pV = constant ⇒ slope =dpdV=−PV
& for adiabatic process, Pvγ = constant ⇒dpdV=−γpV⇒x=γ
Similar Questions
One mole of a diatomic ideal gas (γ=1.4) is taken through a cyclic process starting from point A. The process A→B is an adiabatic compression, B→C is isobaric expansion, C→D is an adiabatic expansion, and D→A is isochoric. The volume ratios are VA/VB=16andVC/VB=2 and the temperature at A is TA=300K. Calculate the temperature of the gas at the points B and D and find the efficiency of the cycle.
View SolutionA gas follows PV12=constant as shown. If V2=2V1 , find T2T1
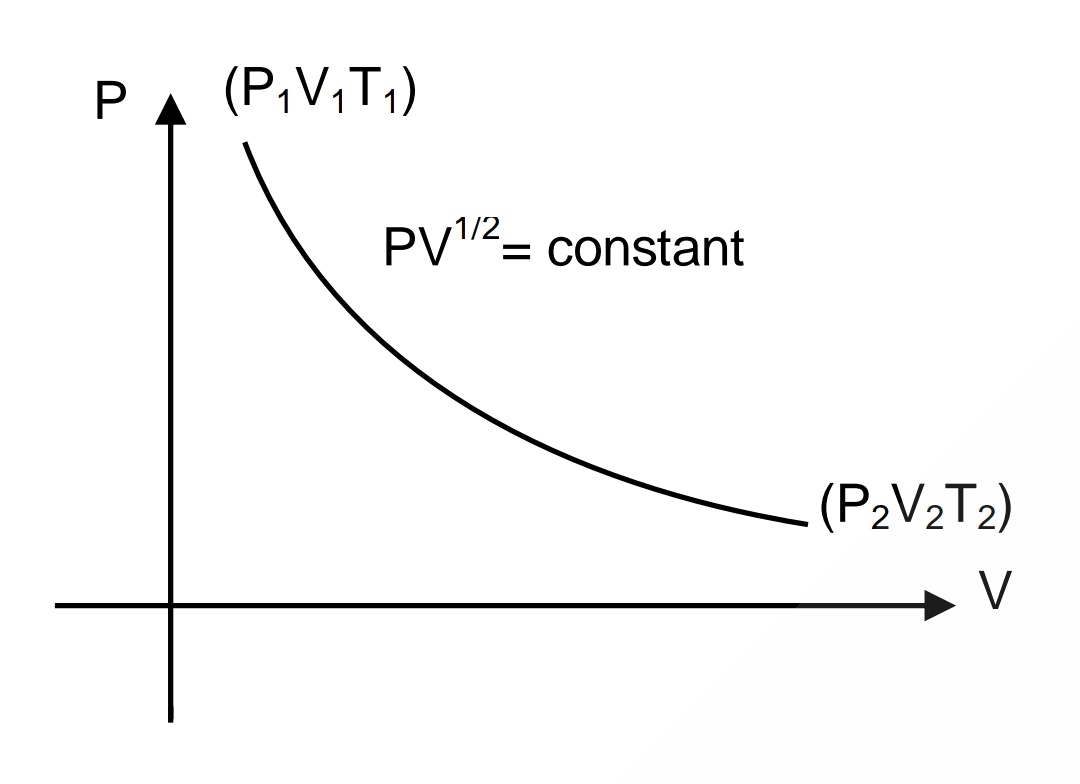
View Solution
Knowledge Check
Two different adiabatic parts for the same gas intersect two isothermals at T1andT2 shown in P-V diagram . Then the ratio of VaVb will be
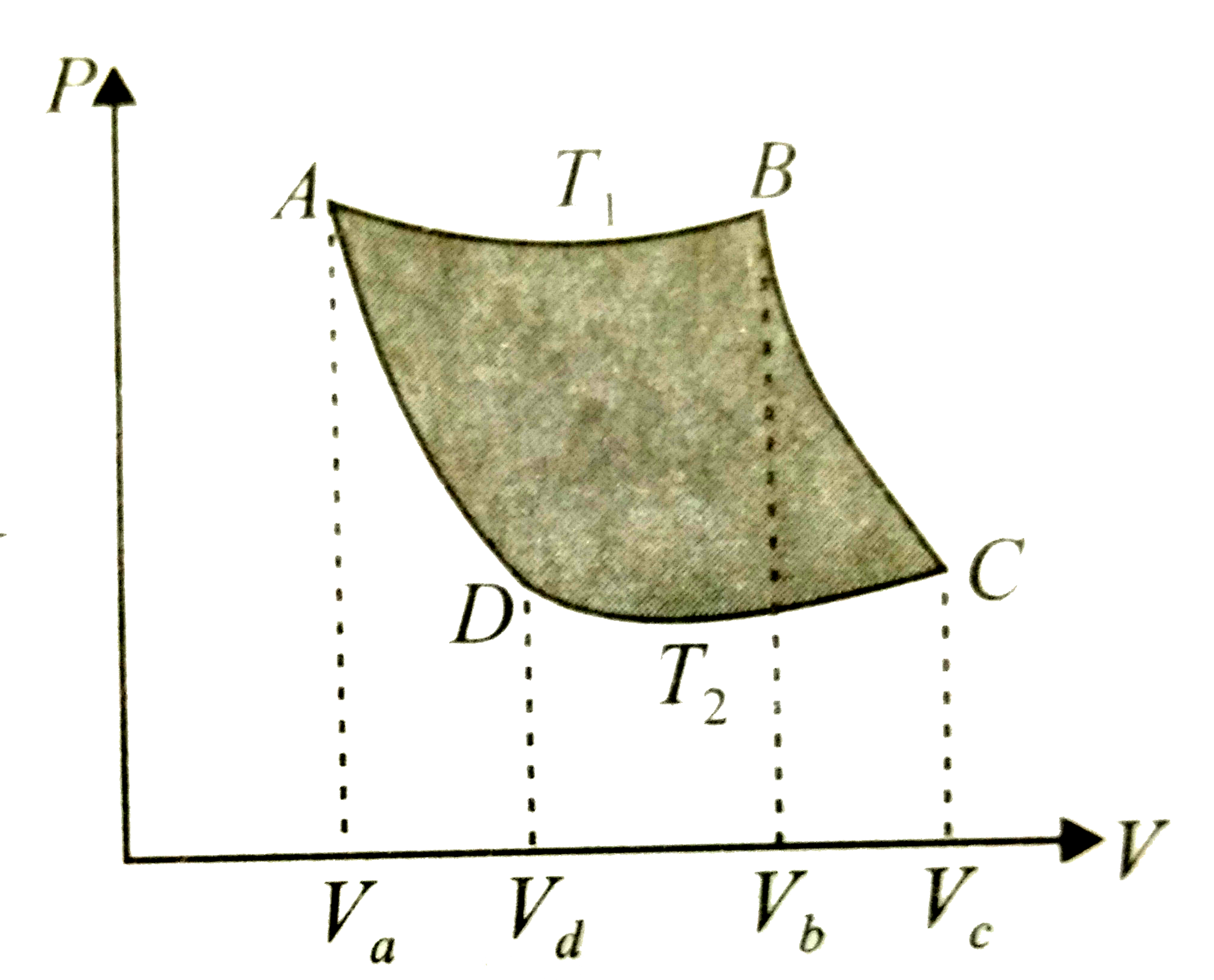 AVcVdBVdVcCγVdVcD1γVdVc
AVcVdBVdVcCγVdVcD1γVdVcThe temperature of an ideal gas undergoing adiabatic expansion varies with volume as T∝V−34, then the value of CPCV for the gas is
A35B53C73D74A monotomic ideal gas of two metal is taken through a cyclic process straining from A as shown VB/VA=2andVD/VA=4 Temperature TAis27∘C
The work done during the process C→D is
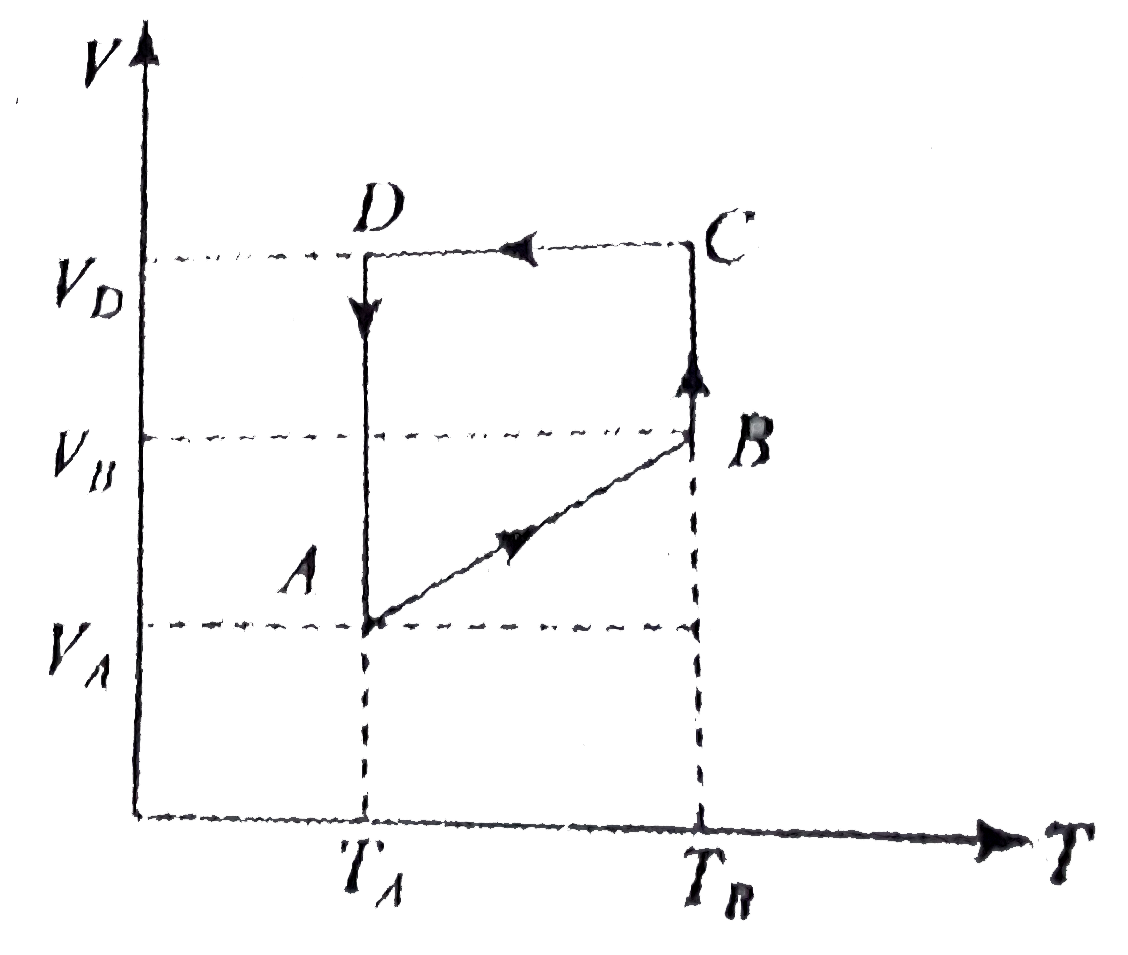 A900R (absorbed)B900R(released)C1200R(absorbed)D1200R(released)
A900R (absorbed)B900R(released)C1200R(absorbed)D1200R(released)
Draw the P-T and V-T diagrams for an isobaric process of expansion, corresponding to n moles of an ideal gas at pressure P0 from V0 to 2V0
View SolutionThe temperature of an ideal gas undergoing adiabatic expansion varies with volume as T∝V−34, then the value of CPCV for the gas is
View SolutionA monotomic ideal gas of two metal is taken through a cyclic process straining from A as shown VB/VA=2andVD/VA=4 Temperature TAis27∘C
The work done during process B→C (approx) is
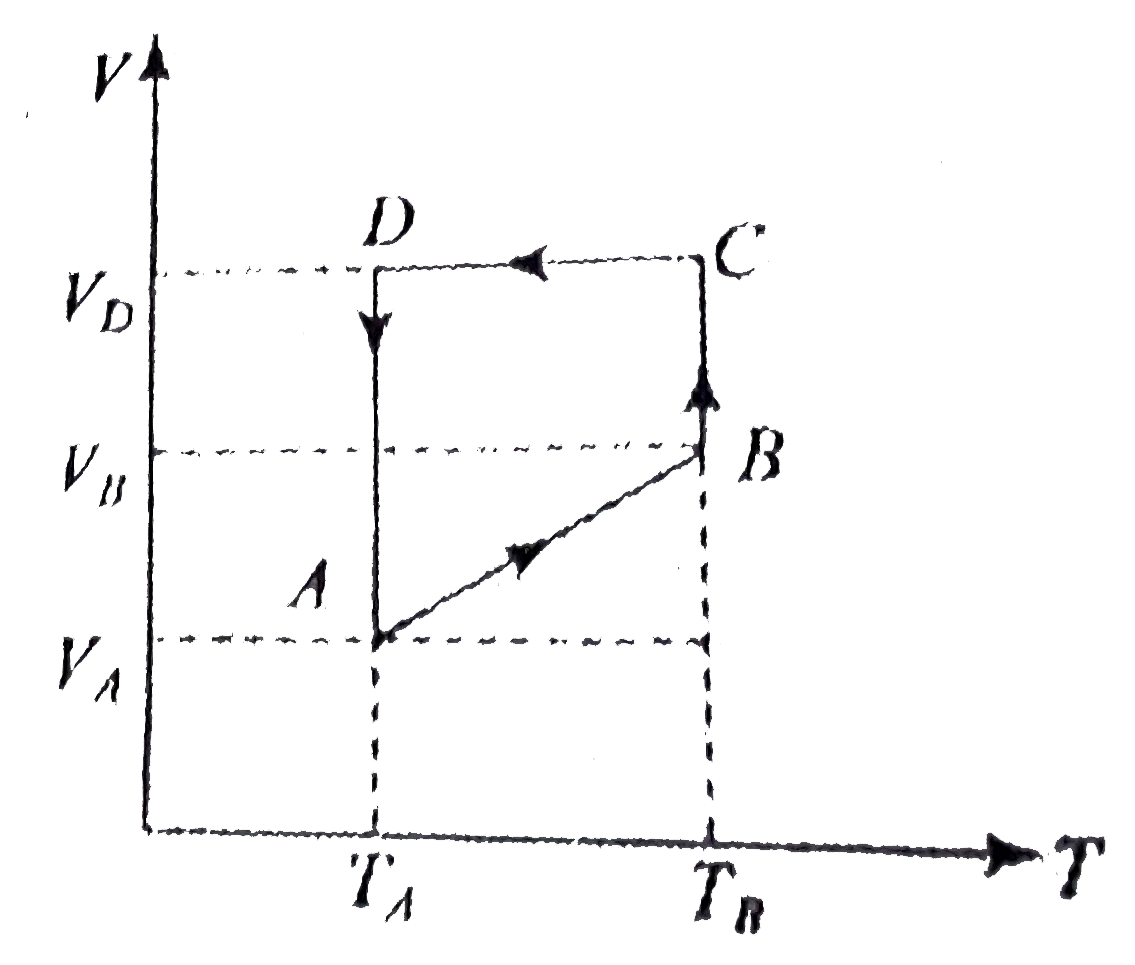
View SolutionA monotomic ideal gas of two metal is taken through a cyclic process straining from A as shown VB/VA=2andVD/VA=4 Temperature TAis27∘C
The work done during the process D→A is
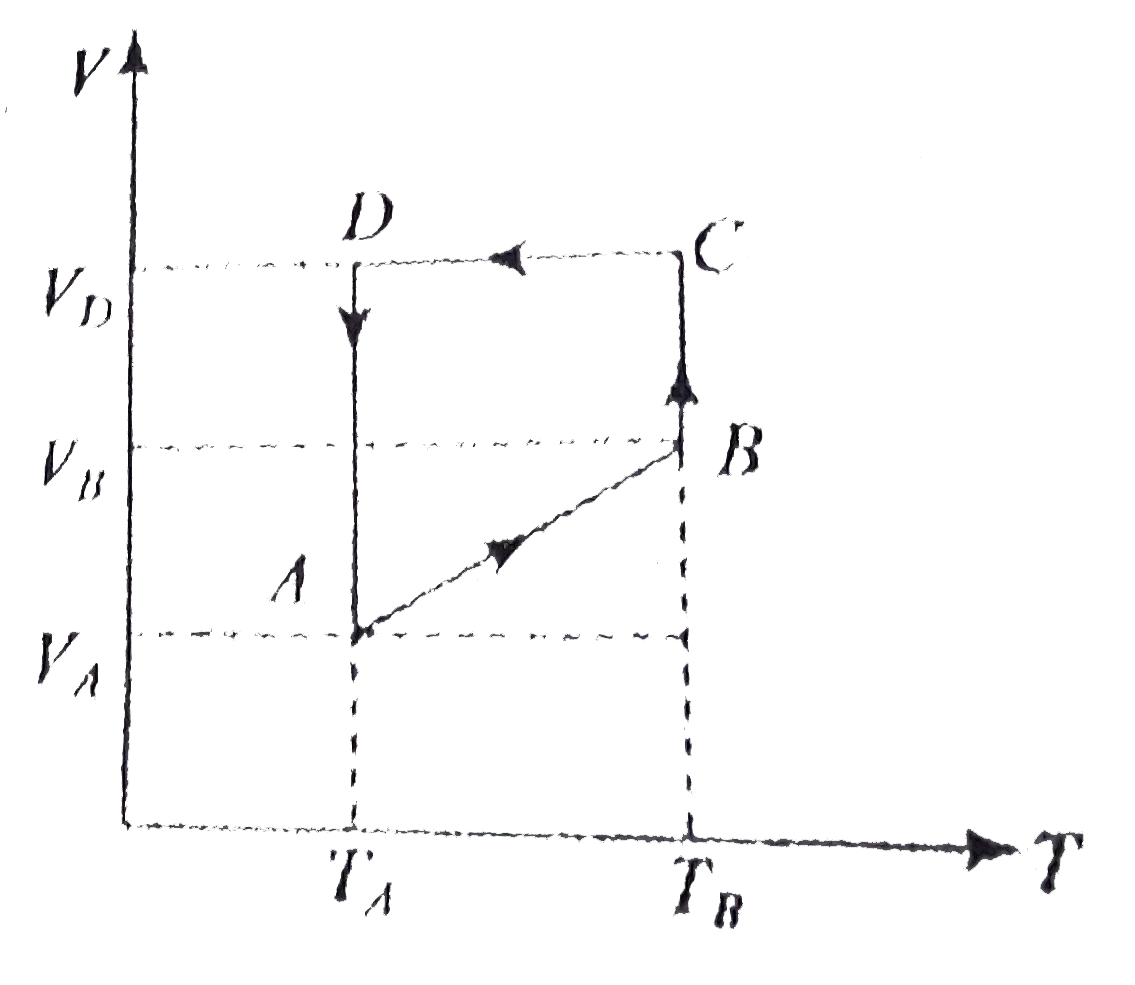
View SolutionThe temperature of an ideal gas undergoing adiabatic expansion varies with volume as T∝V−34, then the value of CPCV for the gas is
View Solution
