If a system undergoes an adiabatic change from state 1 to state 2, the work done by the gas is:
The correct Answer is:A
To determine the work done by the gas during an adiabatic change from state 1 to state 2, we can follow these steps:
1. Understand the Adiabatic Process:
- In an adiabatic process, there is no heat exchange between the system and its surroundings. This means that the heat (q) is equal to zero.
2. Apply the First Law of Thermodynamics:
- The first law of thermodynamics states:
q=ΔU+W
where q is the heat added to the system, ΔU is the change in internal energy, and W is the work done by the system.
3. Substitute for Adiabatic Process:
- Since q=0 for an adiabatic process, we can rewrite the equation as:
0=ΔU+W
4. Rearrange the Equation:
- Rearranging the equation gives us:
W=−ΔU
5. Define Change in Internal Energy:
- The change in internal energy (ΔU) can be expressed as:
ΔU=U2−U1
where U1 is the internal energy at state 1 and U2 is the internal energy at state 2.
6. Substitute ΔU into the Work Equation:
- Now, substituting ΔU into the work equation gives:
W=−(U2−U1)=U1−U2
7. Conclusion:
- Therefore, the work done by the gas during the adiabatic process from state 1 to state 2 is:
W=U1−U2
- In an adiabatic process, there is no heat exchange between the system and its surroundings. This means that the heat (q) is equal to zero.
- The first law of thermodynamics states:
q=ΔU+W
where q is the heat added to the system, ΔU is the change in internal energy, and W is the work done by the system.
- Since q=0 for an adiabatic process, we can rewrite the equation as:
0=ΔU+W
- Rearranging the equation gives us:
W=−ΔU
- The change in internal energy (ΔU) can be expressed as:
ΔU=U2−U1
where U1 is the internal energy at state 1 and U2 is the internal energy at state 2.
- Now, substituting ΔU into the work equation gives:
W=−(U2−U1)=U1−U2
- Therefore, the work done by the gas during the adiabatic process from state 1 to state 2 is:
W=U1−U2
Similar Questions
shows three paths through which a gas can be taken from the state A to the state B. calculate the work done by the gas in each of the three paths.
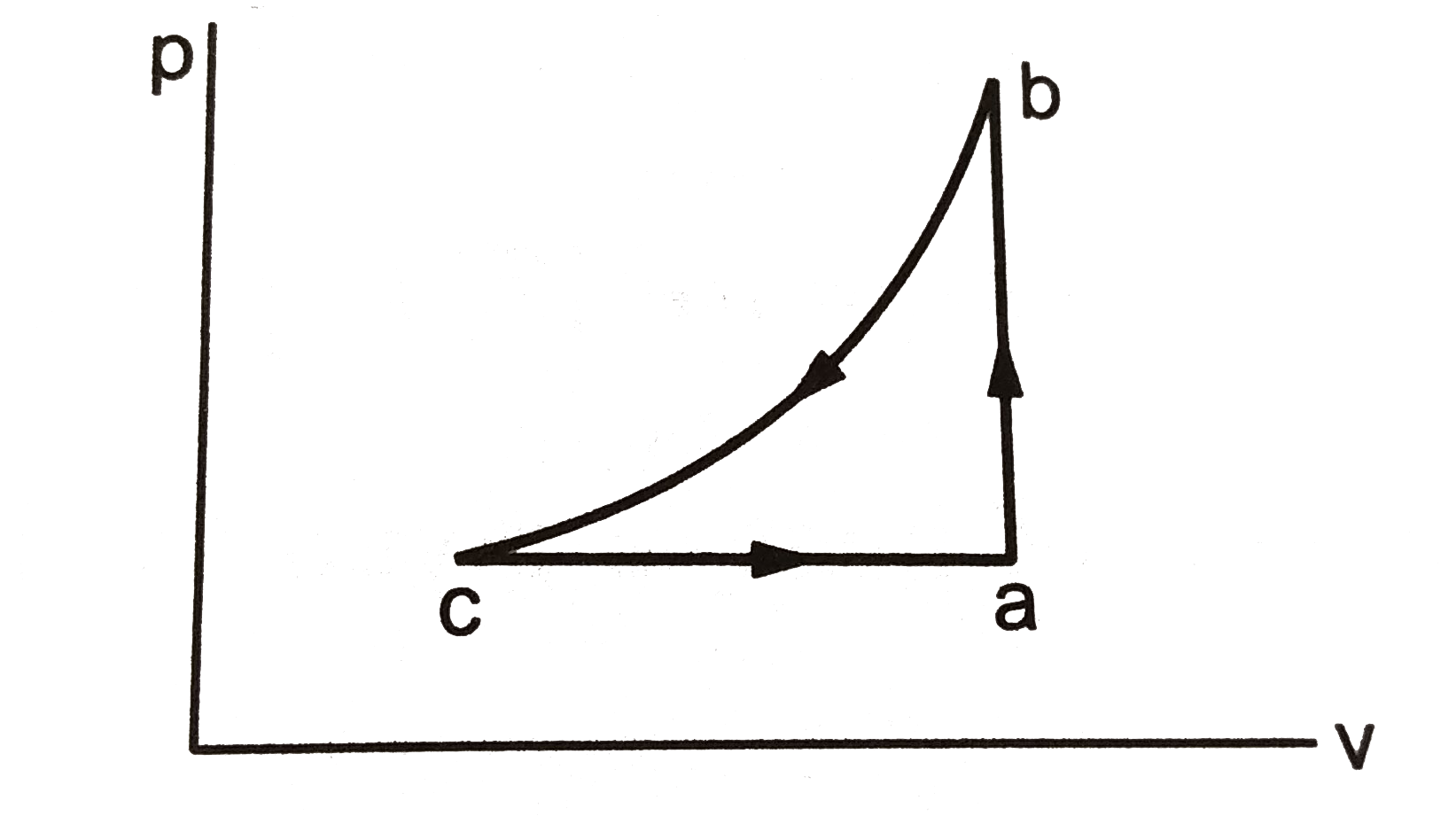
View Solution
As shown in figure three paths through which a gas can be taken from the state A to the state B. Calculate the work done by the gas in each of the three paths.View Solution
Knowledge Check
- Question 1 - Select One
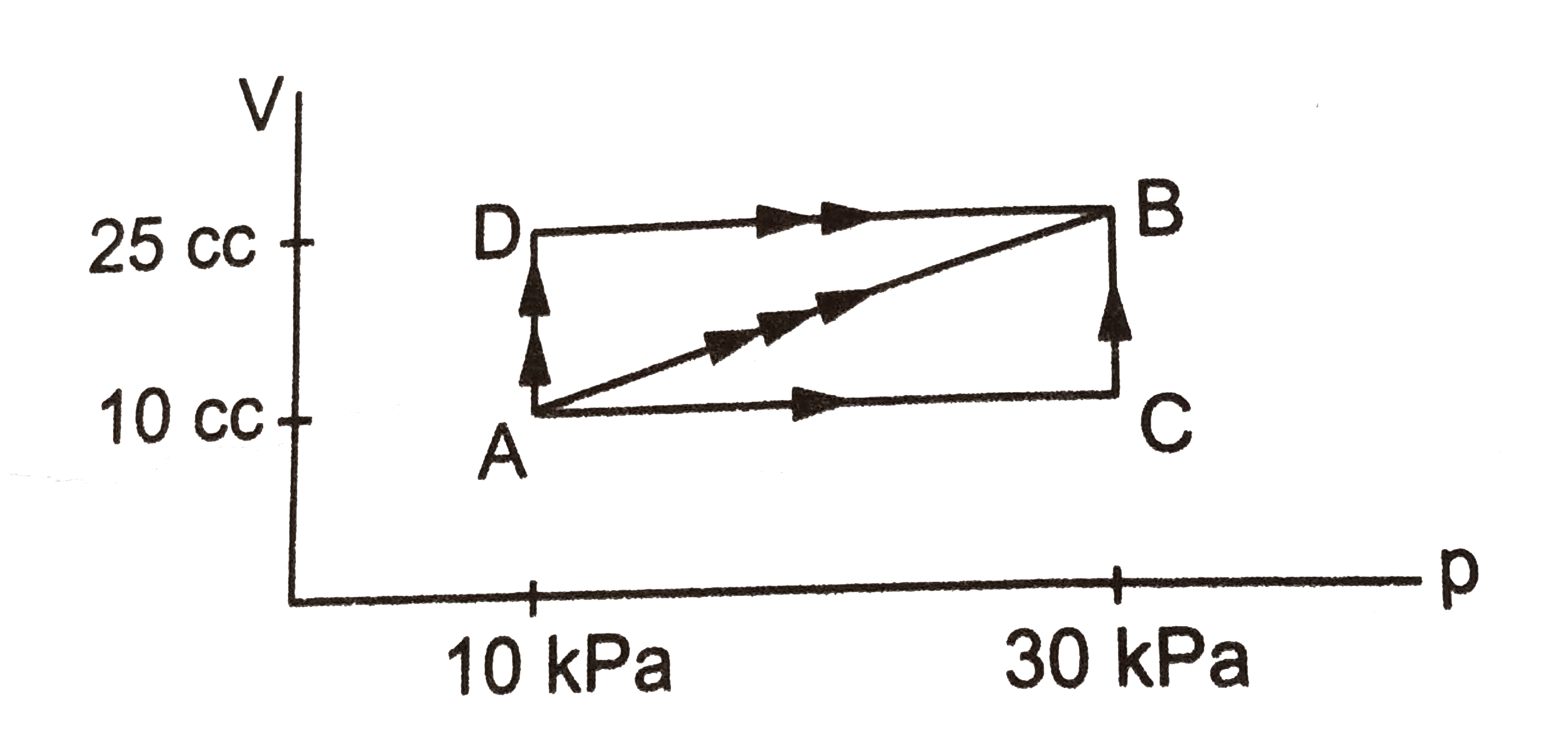
An ideal gas change from state a to state b as shown in Fig. what is the work done by the gas in the process?
AZeroBPositiveCNegativeDInfinite - Question 2 - Select One
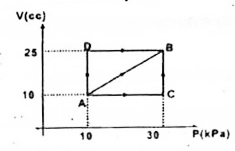
An ideal gas change from state a to state b as shown in Fig. what is the work done by the gas in the process?
AzeroBpositiveCnegativeDinfinite - Question 3 - Select One
One mole of a gas in the state A(P1,V1,T1) is subjected to adiabatic expansion to attain state B(P2,V2,T2). The work done by the gas is:
A−R(T1−T2)γ−1BnR(T2−T1)γ−1CR(T2−T1)1−γDP2V2−P1V11−γ
Figure shows three paths through which a gas can be taken from the state A to the state B. Calculate the work done by the gas in each of the three paths.
View SolutionThe P - V diagram of a system undergoing thermodynamic changes is as shown in the figure. The work done by the system in going from A→B→C is 30 J. If 68 J of heat is given to the system, then the change in the internal energy of the system between A and C is
View SolutionAn ideal gas system undergoes an isothermal process, then the work done during the process is
View SolutionAn ideal gas system undergoes an isothermal process, then the work done during the process is
View SolutionIf a system undergoes contraction of volume then the work done by the system will be
View Solution