A force F=-4x+8 (in N) is acting on a block where x is the position of the block in metres. The energy of oscillation is 32 J. The block oscillates between two points, out of which the value of position of one point (in metres) is an integer from 0 to 9. Find it.
The correct Answer is:6
To solve the problem step by step, we can follow these instructions:
Step 1: Understand the Force Equation
The force acting on the block is given by the equation:
F=−4x+8
This indicates that the force is a function of the position x.
Step 2: Find the Mean Position
The mean position (equilibrium position) occurs when the force F is zero. Setting the force equation to zero:
−4x+8=0
Solving for x:
4x=8
x=2
Thus, the mean position is x=2 meters.
Step 3: Identify the Spring Constant
From the force equation, we can identify the spring constant k:
F=−kx
Comparing with our equation:
k=4N/m
Step 4: Use the Energy Equation
The total mechanical energy E in simple harmonic motion is given by:
E=12kA2
where A is the amplitude. Given that the energy E is 32 J, we can set up the equation:
32=12×4×A2
Step 5: Solve for Amplitude
Rearranging the energy equation to solve for A2:
32=2A2
A2=322=16
Taking the square root:
A=4m
Step 6: Determine the Oscillation Points
The block oscillates around the mean position x=2 with an amplitude of 4 meters. Therefore, the maximum and minimum positions are:
- Maximum position:
xmax=2+4=6m
- Minimum position:
xmin=2−4=−2m
Step 7: Identify Valid Positions
Since the problem specifies that one of the positions must be an integer between 0 and 9, we can see that:
- The valid position within this range is 6m.
Final Answer
The position of one point where the block oscillates is:
6m
---
The force acting on the block is given by the equation:
F=−4x+8
This indicates that the force is a function of the position x.
The mean position (equilibrium position) occurs when the force F is zero. Setting the force equation to zero:
−4x+8=0
Solving for x:
4x=8
x=2
Thus, the mean position is x=2 meters.
From the force equation, we can identify the spring constant k:
F=−kx
Comparing with our equation:
k=4N/m
The total mechanical energy E in simple harmonic motion is given by:
E=12kA2
where A is the amplitude. Given that the energy E is 32 J, we can set up the equation:
32=12×4×A2
Rearranging the energy equation to solve for A2:
32=2A2
A2=322=16
Taking the square root:
A=4m
The block oscillates around the mean position x=2 with an amplitude of 4 meters. Therefore, the maximum and minimum positions are:
- Maximum position:
xmax=2+4=6m
- Minimum position:
xmin=2−4=−2m
Since the problem specifies that one of the positions must be an integer between 0 and 9, we can see that:
- The valid position within this range is 6m.
The position of one point where the block oscillates is:
6m
Similar Questions
In the given arrangement the block is released from the position where the spring is unstretched. The speed of the block when it has descended through 2cm is x10. Find the value of x.

View SolutionAt t = 0 the positions of two blocks are shown. Their is no external force acting on the system. Find the coordinates of center of mass of the system at t = 3 second :
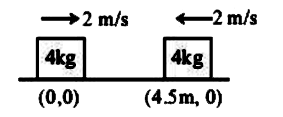
View Solution
Knowledge Check
A force F=−kx3 is acting on a block moving along x-axis. Here, k is a positive constant. Work done by this force is
Apositive in displacing the block from x = 3 to x = 1Bpositive in displacing the block from x = - 1 to x = - 3Cnegative in displacing the block from x = 3 to x = 1Dnegative in displacing the block from x = - 1 to x = - 3For SHM to take place force acting on the body should be proportional to −x or F=−kx. If A be the amplitude then enegry of oscillation is 1/2KA2.
If enegry of oscillation is 18J, between what points does the block will oscillate?Abetween x=0 nad x=4mBbetween x=−1m and x=5mCbetween x=−2 and x=6mDbetween x=1m and x=3mPassage IX) For SHM to take place force acting on the body should be proportional to -x or F = -kx. If A be the amplitude then energy of oscillation is 12kA2
Force acting on a block is F=(−4x+8). Here F is in Newton and x the position of block on x-axis in meterAmotion of the block is periodic but not simple harmonicBMotion of the block is not periodicCmotion of the block is simple harmonic about origin, x=0Dmotion of the block is simple harmonic about x=2m.
The block in Fig. 8-12a lies on a horizontal frictionless surface, and the spring constant is 50 N/m. Initially, the spring is at its relaxed length and the block is stationary at position x=0. Then an applied force with a constant magnitude of 3.0 N pulls the block in the positive direction of the x axis, stretching the spring until the block stops. When that stopping point is reached, what are (a) the position of the block, (b) the work that has been done on the block by the spring force ? During the block's displacement, what are (d) the block's position when its kinetic energy is maximum and (e) the value of that maximum kinetic energy ?
View SolutionIf the position of the block in a block-spring oscillator is given by
x(t)=(3.00×10−3m)cos[(4.00rad/s)t+0.120rad], what is the block's position, velocity and acceleration at time t= 2.30s?
View SolutionFor SHM to take place force acting on the body should be proportional to −x or F=−kx. If A be the amplitude then energy of oscillation is 1/2KA2.
Force acting on a block is F=(−4x+8). Here F is in newton and x in the position of block on x-axis in meters
View SolutionPassage IX) For SHM to take place force acting on the body should be proportional to -x or F = -kx. If A be the amplitude then energy of oscillation is 12kA2
If energy of osciallation is 18 J, between what points the block will oscillate?
View SolutionA force F=(3xˆi+4ˆj) Newton (where x is in metres) acts on a particle which moves from a position (2m, 3m) to (3m, 0m). Then the work done is
View Solution
