body moves along x-axis with velocity v = 5 sin(2t)m/s starting from xi=−2.5mRatio of displacement to distance traveled by body from t=0stot=3π/2sec is :
1:1
0
1:3
1:2
The correct Answer is:C
To solve the problem, we need to find the ratio of displacement to distance traveled by a body moving along the x-axis with a given velocity function. The velocity function is given as v(t)=5sin(2t) m/s, and the body starts from an initial position of xi=−2.5 m. We will analyze the motion from t=0 s to t=3π2 s.
1. Identify the Velocity Function:
The velocity of the body is given by:
v(t)=5sin(2t)
2. Determine the Time Intervals:
We need to find the points in time when the velocity is zero, as this will help us determine the intervals of motion. The velocity is zero when:
5sin(2t)=0⟹sin(2t)=0
This occurs at:
2t=nπ(n∈Z)⟹t=nπ2
For n=0,1,2,3, we find:
- t=0
- t=π2
- t=π
- t=3π2
3. Calculate Displacement:
Displacement can be calculated by integrating the velocity function over the time interval from t=0 to t=3π2:
Displacement=∫3π20v(t)dt=∫3π205sin(2t)dt
To solve this integral:
=5(−12cos(2t))3π20=−52(cos(3π)−cos(0))
=−52(−1−1)=−52×(−2)=5 m
4. Calculate Distance Traveled:
The distance traveled is the total area under the velocity-time graph, considering the absolute value of the velocity. We need to calculate the area for each segment where the velocity is positive and negative:
- From t=0 to t=π2 (positive velocity).
- From t=π2 to t=π (negative velocity).
- From t=π to t=3π2 (positive velocity).
The distance can be calculated as:
Distance=∫π205sin(2t)dt+∣∣
∣∣∫ππ25sin(2t)dt∣∣
∣∣+∫3π2π5sin(2t)dt
Each of these integrals evaluates to:
∫5sin(2t)dt=−52cos(2t)
Evaluating each segment:
- From 0 to π2: 5 m (positive area)
- From π2 to π: 5 m (negative area, but we take absolute value)
- From π to 3π2: 5 m (positive area)
Thus, the total distance traveled is:
Distance=5+5+5=15 m
5. Calculate the Ratio of Displacement to Distance:
Finally, we find the ratio of displacement to distance:
Ratio=DisplacementDistance=515=13
Final Answer:
The ratio of displacement to distance traveled by the body from t=0 s to t=3π2 s is 13.
The velocity of the body is given by:
v(t)=5sin(2t)
We need to find the points in time when the velocity is zero, as this will help us determine the intervals of motion. The velocity is zero when:
5sin(2t)=0⟹sin(2t)=0
This occurs at:
2t=nπ(n∈Z)⟹t=nπ2
For n=0,1,2,3, we find:
- t=0
- t=π2
- t=π
- t=3π2
Displacement can be calculated by integrating the velocity function over the time interval from t=0 to t=3π2:
Displacement=∫3π20v(t)dt=∫3π205sin(2t)dt
To solve this integral:
=5(−12cos(2t))3π20=−52(cos(3π)−cos(0))
=−52(−1−1)=−52×(−2)=5 m
The distance traveled is the total area under the velocity-time graph, considering the absolute value of the velocity. We need to calculate the area for each segment where the velocity is positive and negative:
- From t=0 to t=π2 (positive velocity).
- From t=π2 to t=π (negative velocity).
- From t=π to t=3π2 (positive velocity).
Distance=∫π205sin(2t)dt+∣∣
∣∣∫ππ25sin(2t)dt∣∣
∣∣+∫3π2π5sin(2t)dt
Each of these integrals evaluates to:
∫5sin(2t)dt=−52cos(2t)
Evaluating each segment:
- From 0 to π2: 5 m (positive area)
- From π2 to π: 5 m (negative area, but we take absolute value)
- From π to 3π2: 5 m (positive area)
Distance=5+5+5=15 m
Finally, we find the ratio of displacement to distance:
Ratio=DisplacementDistance=515=13
The ratio of displacement to distance traveled by the body from t=0 s to t=3π2 s is 13.
Similar Questions
A body starting from rest has an acceleration of 5m/s2. Calculate the distance travelled by it in 4th second.
View SolutionA particle is moving along the x-axis such that s=6t−t2, where s in meters and t is in second. Find the displacement and distance traveled by the particle during time interval t=0 to t=5s.
View Solution
Knowledge Check
- Question 1 - Select One or More
body moves along x-axis with velocity v = 5 sin(2t)m/s starting from xi=−2.5m
Which of the following statements are correct ?ABody crosses the origin twice in 2πsecBBody crosses the origin 4 times in 2πsecCTotal displacement of body in 2πsecis5mDTotal displacement of body in 2πsec is 0 - Question 2 - Select One
body moves along x-axis with velocity v = 5 sin(2t)m/s starting from xi=−2.5m
Total distance traveled by the body with its acceleration directed along +ve x-axis in 3π/2 sec will be :A7.5mB5mC2.5mD10 m - Question 3 - Select One
A: A body is moving along a straight line such that its velocity varies with time as shown in figure. Magnitude of displacement of the body from t=0 to t=12s is the same as the distance travelled by it in the given time duration,
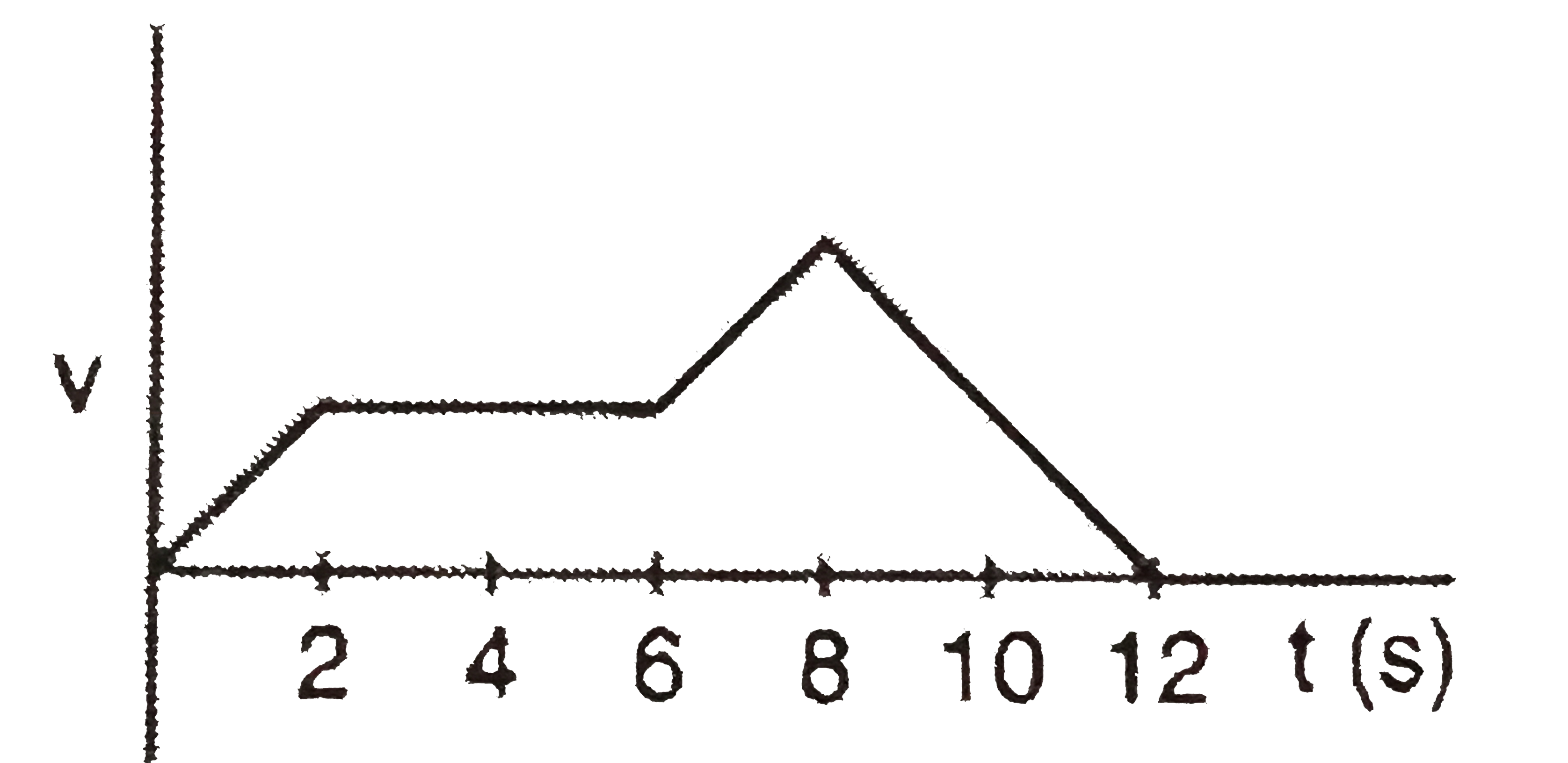
R: For a unidirectional motion of a body, |displacement| = distanceAIf both A and B are true and R is the correct explanation of ABIf both A and R are true but R is not correct explantion of ACIf A is true but R is falseDIf A is false but R is true
Assertion : A body is moving along a straight line such the its velocity varies with a time as shown in figure. Magnmitude of displacement of the body from t = 0 to t = 12 s is the same as the distance travelled by it in the given time duration.

Reason : For unidirectional motion of a body,
|displacement|=distanceView SolutionFind the distance travelled by a body having velocity v=1−t2 from t = 0 tol t = 2 sec .
View SolutionIn the given v-t graph, the distance travelled by the body in 5 sec will be :
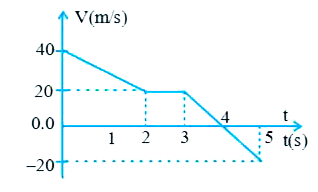 View Solution
View SolutionThe position of a body moving along x-axis at time t is given by x=(t2−4t+6)m. The distance travelled by body in time interval t = 0 to t = 3 s is
View SolutionA particle moves along the x - axis according to x=A[1+sinωt]. What distance does is travel in time interval from t=0 to t=2.5π/ω ?
View Solution

