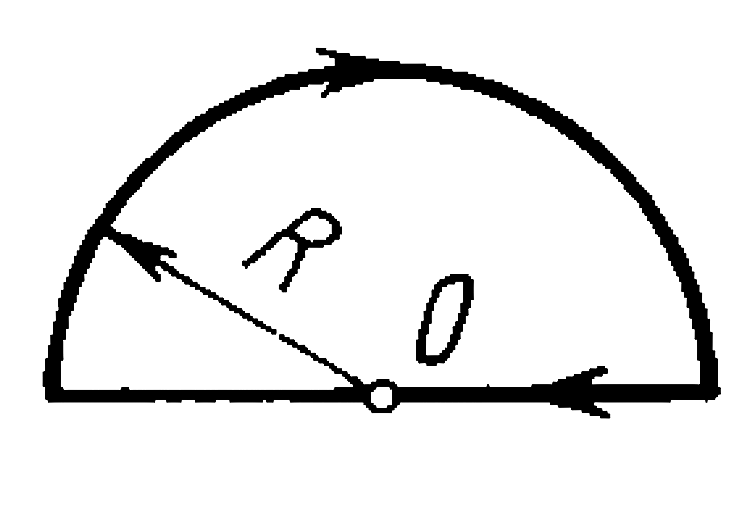
The magnitude of the force vector acting on a unit length of a thin wire carrying a current I =8A at a point O , if the wire is bent as shown in the figure with a radius R =10π cm, is

64μN/m
32μN/m
20μN/m
100μN/m
The correct Answer is:A
Given,

R=10πcm =10π×10−2 m
I=8A
Magnitude of the force vector acting on thin wire is given by ,
F=IB
⇒ F=8B ….(1)
Magnetic field produced by the thin wire at centre O is given by ,
B=μ0I4R
=(4π×10−7)×84×10π×10−2
=8×10−710×10−2
B=8×10−6 T
Substituting B value in equation (1) ,
⇒F=8×8×10−6
=64×10−6
∴F=64μN/m
Topper's Solved these Questions
- EAMCET-2019 (TS) SHIFT-1BOOK - SIA PUBLICATIONCHAPTER - EAMCET-2019 (TS) SHIFT-1EXERCISE - CHEMISTRY
10 Videos
- EAMCET-2019 (TS) SHIFT-1BOOK - SIA PUBLICATIONCHAPTER - EAMCET-2019 (TS) SHIFT-1EXERCISE - CHEMISTRY
10 Videos
- EAMCET QUESTION PAPER 2017BOOK - SIA PUBLICATIONCHAPTER - EAMCET QUESTION PAPER 2017EXERCISE - CHEMISTRY
6 Videos
- FUNCTIONS AND MATHEMATICAL INDUCTION BOOK - SIA PUBLICATIONCHAPTER - FUNCTIONS AND MATHEMATICAL INDUCTION EXERCISE - Problems
58 Videos
Similar Questions
Find the magtiude and direction of a force vector acting on a unit length of a thin wire, carrying a current I=8.0A, at a point O. If the wire is hent as shown in (a) Fig with curvature radius R=10cm
(b ) Fig the distance between the long parallel segments of the wire being equal to l=20cm.

View SolutionA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

View Solution
Knowledge Check
A long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is
 Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2
Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2A wire A , bent in the shape of an arc of a circle , carrying current of 2 and having radius 2 cm and another wire B, also bent in the shape of arc of a circle , carrying a current of 3 A and having radius of 4 cm , are placed as shown in the figure . The ratio of the magnetic fields due to the wires A and B at the common centre O is :
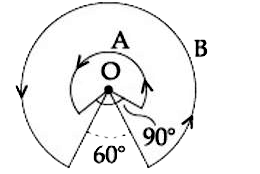 A4:6B6:4C6:5D2:5
A4:6B6:4C6:5D2:5
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius RAμ0l2R(1+3ππ)Bμ0l4R(1+3ππ)Cμ0l8R(1+3ππ)Dμ0l8R(2+3ππ)
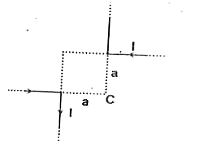
Two inflinitely long wires carrying current I, are bent as shown in the figure. Find the magnetic induction at point C.
View SolutionA wire A , bent in the shape of an arc of a circle , carrying current of 2 and having radius 2 cm and another wire B, also bent in the shape of arc of a circle , carrying a current of 3 A and having radius of 4 cm , are placed as shown in the figure . The ratio of the magnetic fields due to the wires A and B at the common centre O is :

View Solution
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius R
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :

View Solution
