The position of a particle is given by →r=(ˆi+2ˆj−ˆk)momentum →p=(3ˆi+4ˆj−2ˆk)The angular momentum is perpendicular to Solution in Telugu
x-axis
y-axis
z-axis
Line at equal to all the three axes
The correct Answer is:(a)
→r=ˆi+2ˆj−ˆk
→p=3ˆi+4ˆi−2ˆk
Angular momentum,
→l=→r×→p
∣∣
∣
∣∣ˆiˆjˆk12−134−2∣∣
∣
∣∣
=ˆi(−4+4)−ˆj(−2+3)+ˆk(4−6)
=−ˆj−2ˆj
Therefore, the angular momentum is perpendicular x-axis.
Topper's Solved these Questions
Similar Questions
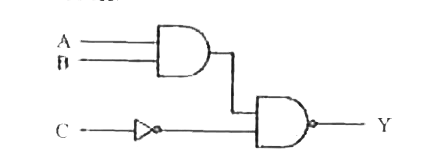
In the following circuit the output Y becomes zero for the input combinations
View SolutionThe specific heat of helium at constant volume is 12.6Jmol−1K−1. The specific heat of helium at constant pressure in Jmol−1K−1 is about
(Assume the temperature of the gas is moderate, universal gas constant, R=8.314Jmol−1K−1
View SolutionThe position of a particle is given by vecr=(hati+2hatj-hatk) and momentum vecp=(3hati+4hatj-2hatk) . The angular momentum is perpendicular to the
View SolutionThe position vector →r and linear momentum →p and →r=ˆi and →p=4ˆj the angular momentum vector is perpendicular to
View Solutionबिंदु (ˆi+2ˆj+ˆk) से जाने वाले समतलो →r⋅(3ˆi−ˆj−ˆk)=1 तथा →r⋅(ˆi+4ˆj−2ˆk)=0 की प्रतिच्छेदन रेखा पर लम्ब समतल का समीकरण ज्ञात कीजिए!
View Solutionबिंदु (ˆi+2ˆj−ˆk) से जाने वाले तथा समतलों →r.(3ˆi−ˆj+ˆk)=1 तथा →r.(ˆi+4ˆj−2ˆk)=0 की प्रतिछेद रेखा पर लम्ब समतल का समीकरण ज्ञात करो।
View Solutionसिद्ध कीजिए कि वे बिंदु जिनके स्थिति सदिश क्रमश : 3ˆi−2ˆj+4ˆk,ˆi+ˆj+ˆk,−ˆi+4ˆj−2ˆk है , समरेख है ।
View Solutionनिम्न रेखा युग्म के बीच का कोण ज्ञात कीजिए →r=(3ˆi+4ˆj−2ˆk)+t(−ˆi+2ˆj+ˆk) तथा →r=(ˆi−7ˆj−2ˆk)+s(ˆi+3ˆj+2ˆk)
View Solutionकिसी कण की स्थिति →r=(ˆi+2ˆj−ˆk) तथा संवेग →P=(3ˆi+4ˆj−2ˆk) है तो कोणीय संवेग निम्न के लम्बवत होगा
View Solutionएक कण की स्थिति →r=(ˆi+2ˆj−ˆk) एवं संवेग →P≡(3ˆi+4ˆj−2ˆk) द्वारा प्रदर्शित होते हैं। कोणीय संवेग लंबवत है
View Solutionकिसी कण की स्थिति. →r=ˆi+2ˆj−ˆk द्वारा दी गई है तथा इसका रेखीय संवेग, →p=3ˆi+4ˆj−2ˆk द्वारा दिया गया है, तो मूल बिन्दु के परितः इसका कोणीय संवेग किसके लम्बवत् होगा?
View SolutionThe position of a particle is given by →r=ˆi+2ˆj−ˆk and its linear momentum is given by →p=3ˆi+4ˆj−2ˆk. Then its angular momentum, about the origin is perpendicular to
View SolutionThe position of a particle is given by →r=(ˆi+2ˆj−ˆk) and momentum →p=(3ˆi+4ˆj−2ˆk). The angular momentum is perpendicular to the
View SolutionFind the shortest distance between two lines whose vector equations are : →r=ˆi−7ˆj−2ˆk+λ(ˆi+3ˆj+2ˆk) and →r=−3ˆi+4ˆj−2ˆk+μ(−ˆi+2ˆj+ˆk)
View SolutionPosition of a particle vecr - (hati+2hatj-hatk) And momentum vecP= (3hati+4hatj-2hatk) Is displayed by The angular momentum is perpendicular.
View Solution
