जैसा चित्र में दिखाया गया है, एक खड़ी होने वाली सीढ़ी के दो पक्षों BA और CA की लम्बाई 1.6m है और इनको A पर कब्ज़ा लगा कर जोड़ा गया है । इन्हें ठीक बीच में 0.5m लंबी रस्सी DE द्वारा बाँधा गया है । सीढ़ी BA के अनुदिश B से 1.2m की दूरी पर स्थित बिंदु F से 40kg का एक भार लटकाया गया है । यह मानते हुए कि फर्श घर्षण रहित है और सीढ़ी का भार उपेक्षणीय है, रस्सी में तनाव और सीढ़ी पर फर्श द्वारा लगाया गया बल ज्ञात कीजिए । (g=9.8m/s2लीजिए )
[संकेत : सीढ़ी के दोनों ओर के संतुलन पर अलग-अलग विचार कीजिए )
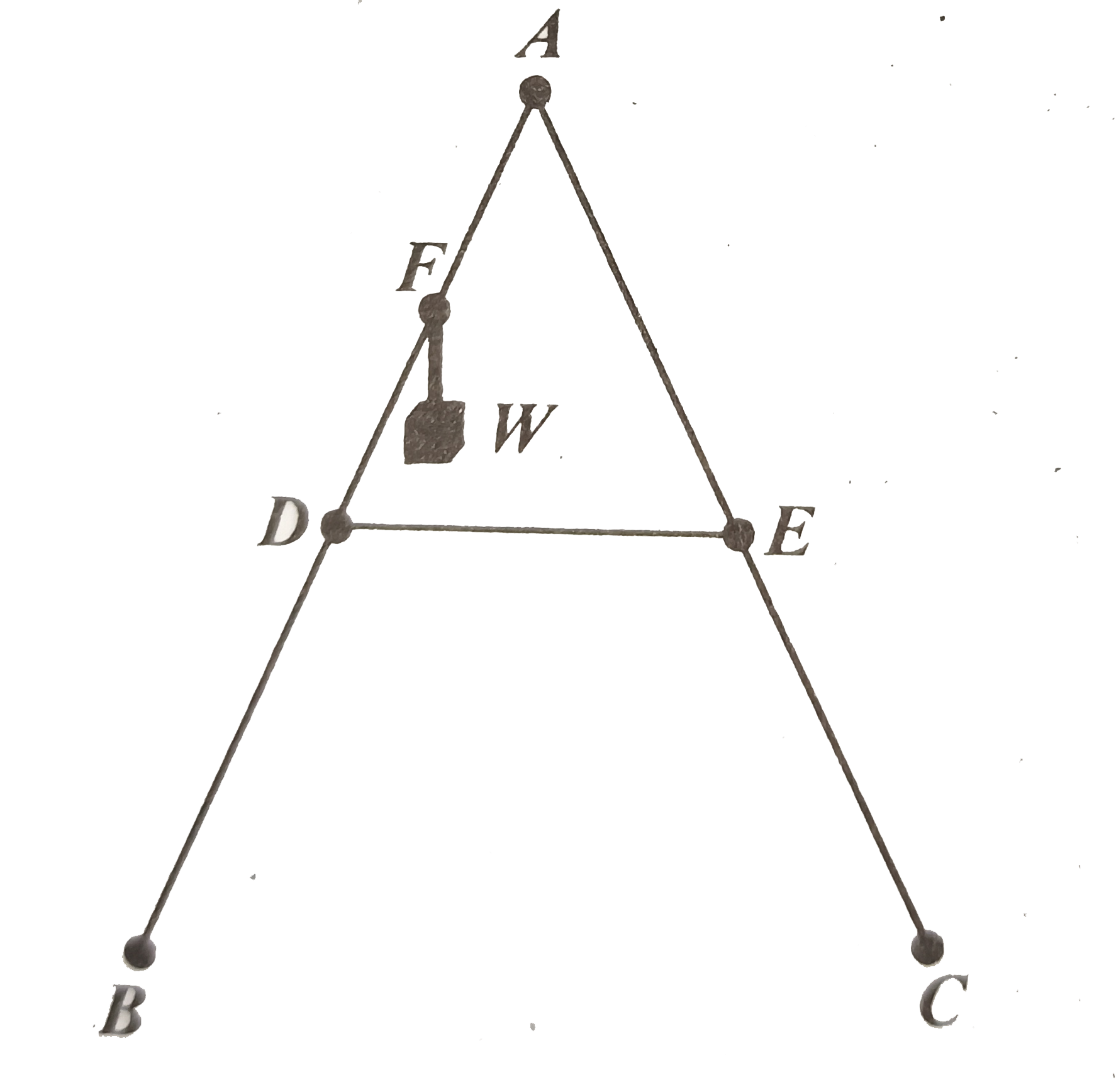
मानलो RB और RC फर्श द्वारा सीढ़ी AB व एक पर आरोपित बल है। T रस्सी DE में उत्पन्न तनाव है।
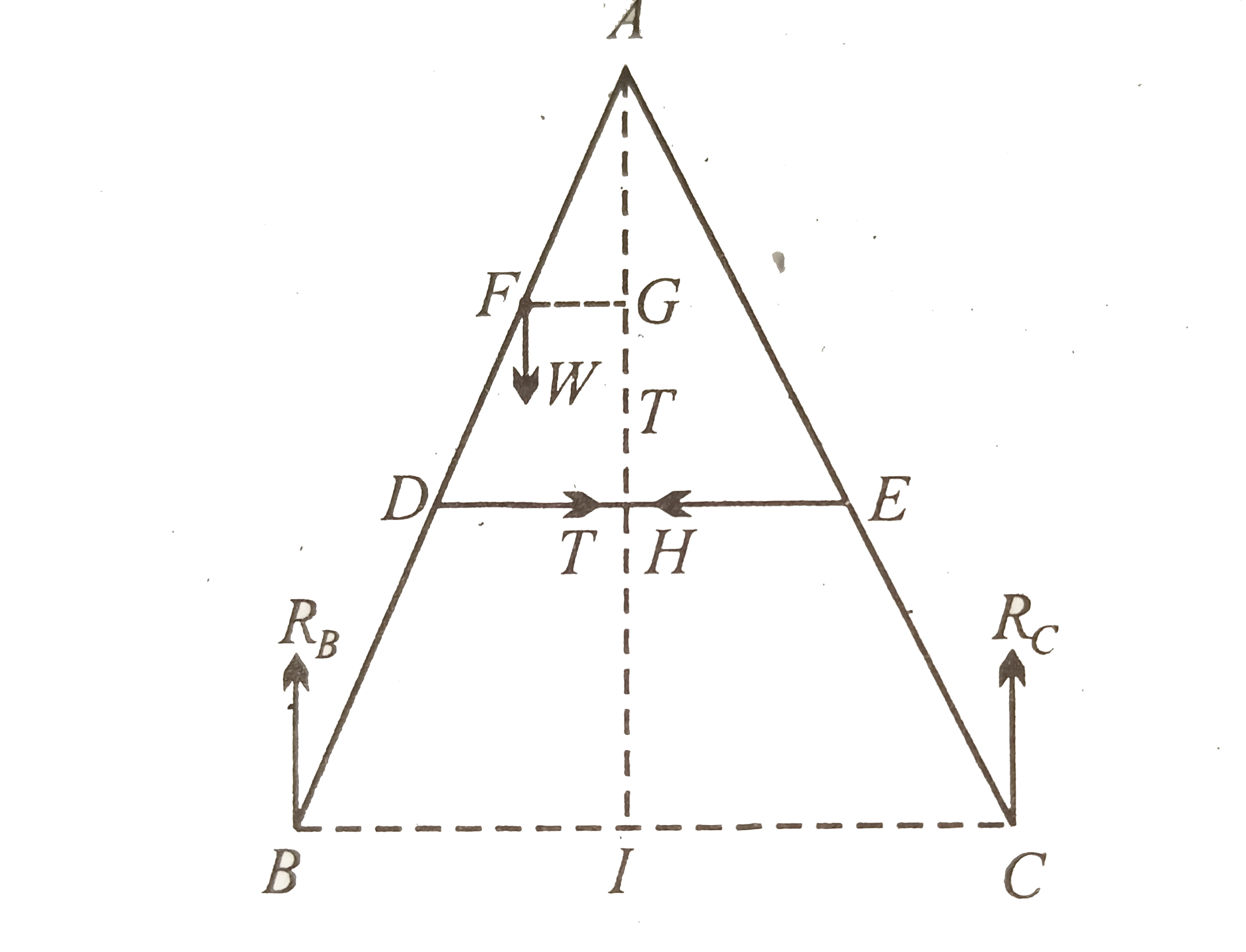
तब रेखीय सन्तुल के लिए,
RA+RB=W
=40g=40×9.8
∴ RA+RB=392 ...(1)
सीढ़ी AC में बिंदु के परितः घूर्णी संतुलन के लिए,
RC×CI=T×AH ...(2)
ज्यामिति से,
BC=2DE=2×0.5=1m
EH=12DE=12×0.5=0.25m,
AE=12AC=12×1.6=0.8m
समकोण ΔAHE में,
AH=√AE2−EH2
=√(0.8)2−(0.25)2
=√0.5775=0.76m
CI=12BC=12×1=0.5m
समी. (2 ) में मान रखने पर,
RC×0.5=T×0.76
या T=0.50.76RC
या T=0.66RC ....(3)
सीढ़ी AB में बिंदु A के परितः घूर्णी संतुलन के लिए,
RB×BI−W×FG=T×AH
BI=12BC=12×1=0.5m
F, AD का मध्य बिंदु है,
∴ FG=12DH=12×0.25=0.125m
समी. (4 ) में मान रखने पर,
RB×0.5−40g×0.125=T×0.76
या RB×0.5−392×0.125=T×0.76
समी. (3 ) से मान रखने पर,
RB×0.5−49=0.66×0.76RC
या RB−98=RC
या RB−RC=98 ...(5)
समी. (1 ) और (5 ) को हल करने पर,
RB=245N तथा RC=147N.
समी (3 ) में मान रखने पर,
T=0.66×147=97N.
Topper's Solved these Questions
- BOOK - NAVBODHCHAPTER - कणों के निकाय की गति और घुर्णो गति EXERCISE - बहुविकल्पीय प्रश्न84videos
कणों के निकाय की गति और घुर्णो गति
- BOOK - NAVBODHCHAPTER - एकसमान वृत्तीय (वर्तुल) गति की गतिकी EXERCISE - NCERT पाठ्यपुस्तक के प्रश्नोत्तर60videos
एकसमान वृत्तीय (वर्तुल) गति की गतिकी
- BOOK - NAVBODHCHAPTER - कार्य, ऊर्जा और शक्ति EXERCISE - NCERT पाठ्यपुस्तक के प्रश्नोत्तर51videos
कार्य, ऊर्जा और शक्ति
Similar Questions
एक समबाहु त्रिभुज ABC का केंद्र O है । F1,F2 और F3 क्रमशः AB, BC व AC के अनुदिश कार्यरत बल हैं । F3 का मान क्या होगा जबकि O के परितः कुल बल - आघूर्ण शून्य है ।
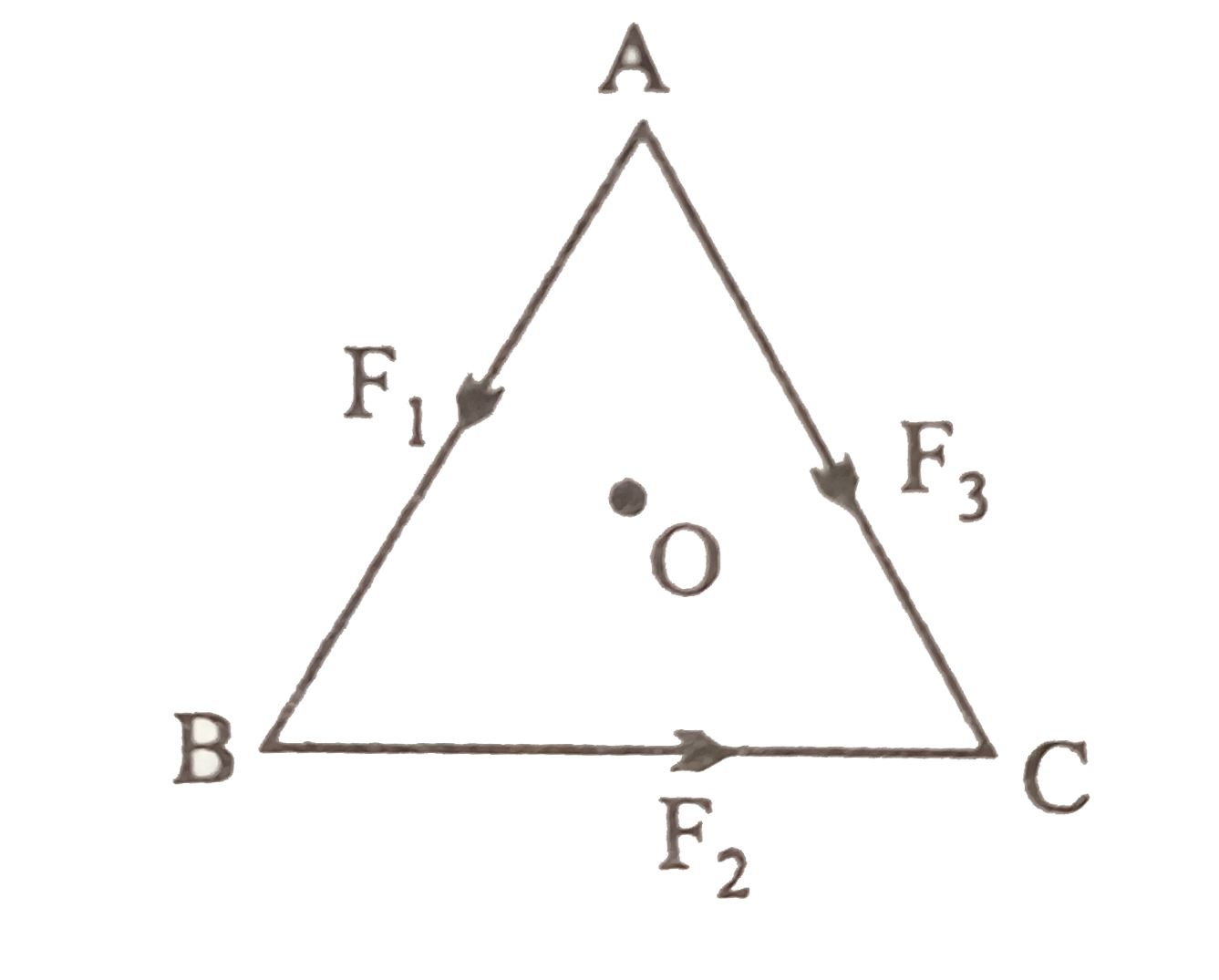 07:15View Solution
07:15View Solutionनिम्नलिखित पर कार्यरत नेट बल का परिमाण व उसकी दिशा लिखिए -
( a ) एकसमान चाल से नीचे गिरती वर्षा की कोई बूँद06:14View Solutionकिसी वस्तु पर किसी बल द्वारा किए गए कार्य का चिह्व समझना महत्वपूर्ण है । सावधानीपूर्वक बताइए कि निम्न लिखित राशियाँ धनात्मक हैं या ऋणात्मक-
( a ) किसी व्यक्ति द्वारा किसी कुँए में से रस्सी से बँधी बाल्टी को रस्सी द्वारा बाहर निकालने में किया गया कार्य ।03:10View Solutionएक टी. वी बनाने के कारखाने में मशीने A,B और C कुल उत्पादन का क्रमशः 30 % और 50 % टी .वी बनाती है। इन मशीनो के उत्पादन का क्रमशः 7% , 5 % और 2% टी . वी खराब (त्रुटिपूर्ण ) पायी जाती है। टी .वी के कुल उत्पादन में से एक टी वी यदृच्छया जाँच के लिए निकाला गया है और वह खराब (त्रुटिपूर्ण ) पाया गया है। इसकी प्रायिकता ज्ञात कीजिए कि वह मशीन A द्वारा बनाया गया है।
02:29View Solutionयह ज्ञात है की महाविद्यालय के छात्रों में से 60 % छात्रावास में रहते है और 40 % छात्रावास में नहीं रहते है । पूर्ववर्ती वर्ष से परिणाम सूचित करते है की छात्रावास में रहने वाले छात्रों में से30 % छात्रों में से 20 % छात्रों ने A ग्रेड लिए। वर्ष के अंत में महाविद्यालय के एक छात्र को यादृच्छया चुना गया और पाया गया की उसे A ग्रेड मिला है । इस बात की क्या प्रायिकता है की वह छात्रावास में रहने वाला है ?
04:06View Solutionताश के 52 पत्तो की एक सुनिश्चित गड्डी में से एक पत्ता यदृच्छया निकाला जाता है | यदि
E : निकाला गया पत्ता हुकुम का है |
F : निकाला गया पत्ता इक्का है , तो E तथा F घटनाएँ है -View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionपद्माकर के पहले कवित्त में किसे शब्द की अधिकाधिक आवृत्ति से चमत्कार उत्पन्न किया गया है ?
View Solutionहस्तक्षेप कविता में क्या दिखाया गया है?
View SolutionMgCO3 के 10g को गर्म करने पर, यह 0.1 मोल CO2 और 4gmgO में अपघटित हो जाता है। MgCO3 की प्रतिशत शुद्धता होगी : (दिया गया है, Mg,C और O के परमाणु भार क्रमशः 24,12 और 16 u है)
View Solutionएक काय केंद्रित घनीय जालक का निर्माण B के खोखले गोलों से किया गया है। ठोस A के गोले, B के खोखले गोलों में उपस्थित है। A की त्रिज्या, B की त्रिज्या की आधी है। एकक कोष्ठिका में, A द्वारा अनअधिधारित B के गोलों के कुल आयतन और एकक कोष्ठिका के आयतन का अनुपात क्या है?
View Solutionनिम्नलिखित में से कौन सा रेखाचित्र एक समभारिक के लिए है: (दिया गया है: (nR)/P gt 1 )
View Solution5 बार और 300K पर एक आदर्श एक्परमाणविक गैस के दो मोल के 1 बार के ब्रह्म डाब तक अनुत्क्रमणीय रूप से प्रसारित किया जाता है गैस दवरा किया गया कार्य xR (बार लीटर में ) है x का मान है
View Solutionरुद्धोष्म और समतापीय स्थितियों के तहत एक आदर्श गैस का उत्क्रमणीय प्रसार चित्र में दिखाया गया है | निम्नलिखित में से कौन सा कथन अशुद्ध है
View Solutionसक्रियण ऊर्जा की गणना के लिए log k बनाम 1/T के बीच का आरेख किसके द्वारा दिखाया गया है?
View Solution

