If l and l'be the lengths of the segment ¯¯¯¯¯PS and ¯¯¯¯¯¯¯P'S of a focal chord ¯¯¯¯¯¯¯¯PP' of the parabola y2=4ax , then show that 1l+1l'=1a . Solution in Bengali
The correct Answer is:=10a⋅1+t21+t2=(1)=1a
Step by step video, text & image solution for If l " and " l' be the lengths of the segment overline(PS) and overline (P'S) of a focal chord overline(PP') of the parabola y^(2) = 4ax , then show that (1)/(l)+(1)/(l')=(1)/(a) . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PARABOLABOOK - CHHAYA PUBLICATIONCHAPTER - PARABOLAEXERCISE - M . C. Q
16 Videos
- PARABOLABOOK - CHHAYA PUBLICATIONCHAPTER - PARABOLAEXERCISE - Very Short Answer Type Qusetions
21 Videos
- ORDER AND DEGREE OF DIFFERENTIAL EQUATION BOOK - CHHAYA PUBLICATIONCHAPTER - ORDER AND DEGREE OF DIFFERENTIAL EQUATION EXERCISE - Sample Questions for Competitive Examination (E Assertion - Reasion Type )
2 Videos
- PERMUTATION AND COMBINATION BOOK - CHHAYA PUBLICATIONCHAPTER - PERMUTATION AND COMBINATION EXERCISE - Sample Questions for Competitive Exams E Assertion -Reason Type
2 Videos
Similar Questions
The length of latus rectum of the parabola 3x2=−8y is _
View SolutionFind the focus, the length of the latus rectum and the directrix of the parabola 3x2=8y
View SolutionStatement - I : The differential equation of curves
represented by y=Aex is given by dydx=y
Statement-II: dydx=y is valid for every member of the given family
View SolutionStatement -I : Number of terms in the expansion of (x+y+z+w)50 is .53C3.
Statement -II : Number of non- negative solution of the equation p+q+r+s=50 is .53C3.
View SolutionIf the length of focal chord of y2=4ax is l, then find the angle between the axis of the parabola and the focal chord.
View SolutionIf P and Q are the end points of a focal chord of the parabola y^(2)=4ax- far with focus isthen prove that (1)/(|FP|)+(1)/(|FQ|)=(2)/(l), where l is the length of semi-latus rectum of the parabola.
View SolutionFor a focal chord PQ of the parabola y2=4ax if SP =l and SQ=l then prove
that 1l+1l+1a.
View SolutionIf ¯aand¯b are the position vectors of the points (1,−1),(−2,m)and¯a,¯b are collinear, then m=
View Solution¯¯¯¯¯¯PQ−¯¯¯¯¯¯TQ+¯¯¯¯¯PS+¯¯¯¯¯ST=
View SolutionIf PQRST is a pentagon, then ¯¯¯¯¯¯PQ+¯¯¯¯¯¯PR+¯¯¯¯¯PS−¯¯¯¯¯¯TQ−¯¯¯¯¯¯TR−¯¯¯¯¯TS=
View SolutionIf ¯a,¯b,¯c are unit vectors such that ¯a⋅¯b=12,¯b⋅¯c=1√2 and ¯c⋅¯a=√32, then ¯a⋅(¯bׯc)=
View SolutionIf l(¯bׯc)+m(¯cׯa)+n(¯aׯb)=0 and at least one of the l, m, n is not zero , then the vectors ¯a,¯b,¯c are
View SolutionThe value of [¯a−¯b¯b−¯c¯c−¯a] where|¯a|=1,∣∣¯b∣∣=2and|¯c|=3 is
View Solution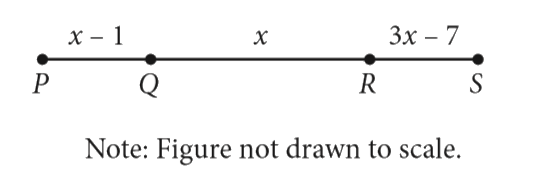
ON ¯¯¯¯¯PS above PQ=RS. What is the length of ¯¯¯¯¯PS?
View Solution¯a,¯b,¯c are three vectors such that |¯a|=1,∣∣¯b∣∣=2,|¯c|=3 and ¯b,¯c are perpendicular . If projection of ¯b on ¯a is the same as the projection of ¯c on ¯a, then ∣∣¯a−¯b+¯c∣∣=
View Solution
