Given the product p of sines of the angles of a triangle and the prodcut q of their cosines, find the cubic equation whos coefficients are functions of p and q. Solution in Bengali
The correct Answer is:z3+(2q−1)z2+(p2+q2−2q)z−q2=0
Step by step video, text & image solution for Given the product p of sines of the angles of a triangle and the prodcut q of their cosines, find the cubic equation whos coefficients are functions of p and q. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - CHHAYA PUBLICATIONCHAPTER - MISCELLANEOUS EXAMPLESEXERCISE - ALGEBRA141videos
MISCELLANEOUS EXAMPLES
- BOOK - CHHAYA PUBLICATIONCHAPTER - MISCELLANEOUS EXAMPLESEXERCISE - COORDINATE GEOMETRY (TWO DIMENSIONAL COORDINATE GEOMETRY)124videos
MISCELLANEOUS EXAMPLES
- BOOK - CHHAYA PUBLICATIONCHAPTER - MISCELLANEOUS EXAMPLESEXERCISE - WBJEE 202623videos
MISCELLANEOUS EXAMPLES
- BOOK - CHHAYA PUBLICATIONCHAPTER - METHOD OF SUBSTITUTIONEXERCISE - Sample Questions for Competitive Examination (Assertion-Reason Type)2videos
METHOD OF SUBSTITUTION
- BOOK - CHHAYA PUBLICATIONCHAPTER - ORDER AND DEGREE OF DIFFERENTIAL EQUATION EXERCISE - Sample Questions for Competitive Examination (E Assertion - Reasion Type )2videos
ORDER AND DEGREE OF DIFFERENTIAL EQUATION
Similar Questions
Solve the equation z2+|Z|=0 where z is a complex quantity.
09:21View SolutionIf O be the origin and if coordinates of any two points Q1andQ2 be (x1,y1)and(x2,y2) respectively, prove that ¯¯¯¯¯¯¯¯OQ1⋅¯¯¯¯¯¯¯¯OQ2cos∠Q1OQ2=x1x2+y1+y2.
09:37View Solution72n+16n−1(n∈N) is divisble by
01:21View SolutionStatement-I: ∫x+1x(1+xex)2dx=11+xex+log∣∣∣xex1+xex∣∣∣+c where c is a real number.
Statement-II: ddx(xex)=(x+1)ex.02:04View SolutionStatement - I : The differential equation of curves
represented by y=Aex is given by dydx=y
Statement-II: dydx=y is valid for every member of the given family03:24View SolutionThe product of the sines of the angles of a triangle is p and the product of their cosines is q. Show that the tangents of the angles are the roots of the equation qx3−px2+(1+q)x−p=0.
04:02View SolutionLet p be the product of the sines of the angles of a triangle ABC and q is the product of the cosines of the angles In this triangle tan A+tan B+tan C is equal to
02:19View Solutionयदिम P,Q से 5 अधिक है और P और Q के वर्गों का योग 55 है तो P तथा Q का गुणनफल ज्ञात करें।
04:58View SolutionWhat is the angle between P and the cross product of (P+Q)and (P-Q) ?
12:24View Solutionएक समकोण त्रिभुज के कर्ण की लम्बाई p सेमि है तथा इसकी एक अन्य भुजा की लम्बाई q सेमि. है |यदि p−q=1 हो,तो इस त्रिभुज की तीसरी भुजा ज्ञात करो|
View SolutionIf the sides of the triangle ABC are p,q and √p2+pq+q2, then the greatest angle of the triangle is-
03:39View SolutionIf the roots of a quadratic equation be p+q and p-q, then find the equation.
02:07View SolutionP∗q=p2−q2
p$q=p2−q2
p$q=p2+q2
p∘q=pq+p+q
pΔq = Remainder of pq
p©q = greatest integer less than or equal to pq.
If p=8andq=10 , then the value of [(p$q)Δ(p∘q)]∗[(q∗p)∘(q©p)] is :02:16View SolutionThe product of the sines of the angles of a triangle is p and the product of their cosines is q. Show that the tangents of the angles are the roots of the equation qx3−px2+(1+q)x−p=0.
02:34View SolutionGiven :
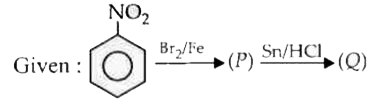
The products P and Q are04:32View Solution

