The corner points of the feasible region determnined by the following system of linear inequalities
0,0
5,0
3,4
0,5
The correct Answer is:C, D
Topper's Solved these Questions
- LINEAR PROGRAMMING GRAPHICAL METHOD BOOK - CHHAYA PUBLICATIONCHAPTER - LINEAR PROGRAMMING GRAPHICAL METHOD EXERCISE - Integer Answer Type
5 Videos
- LINEAR PROGRAMMING GRAPHICAL METHOD BOOK - CHHAYA PUBLICATIONCHAPTER - LINEAR PROGRAMMING GRAPHICAL METHOD EXERCISE - Matrix Match Type
2 Videos
- LINEAR PROGRAMMING GRAPHICAL METHOD BOOK - CHHAYA PUBLICATIONCHAPTER - LINEAR PROGRAMMING GRAPHICAL METHOD EXERCISE - Long Answer Type Question
16 Videos
- LINEAR INEQUATIONSBOOK - CHHAYA PUBLICATIONCHAPTER - LINEAR INEQUATIONSEXERCISE - SAMPLE QUESTION FOR COMPETITIVE EXAMS (Assertion- Reason Type)
2 Videos
- LOGARITHM BOOK - CHHAYA PUBLICATIONCHAPTER - LOGARITHM EXERCISE - Long Answer Type Question
12 Videos
Similar Questions
Knowledge Check
The corner points of the feasible region determined by a system of linear inequations are (0,0),(4,0),(2,4) and (0,5). If the minimum value of Z=ax+by,a, b>0 occurs at (2,4) and (0,5) ,then :
Aa=2bB2a=bCa=bD3a=bFor an objective function Z = ax + by, where a,b>0, the corner points of the feasible region determined by a set of constraints (linear inequalities) are (0, 20). (10, 10), (30, 30) and (0, 40). The condition on a and b such that the maximum z occurs at both the points (30, 30) and (0, 40) is:
Ab−3a=0Ba=3bCa+2b=0D2a−b=0The corner points of the feasible region determined by the system of linear constraints are (0,10) , (5,5) (25,20),(0,30) Let z = px + qy , where p,q>0 Condition on p and q so that te maximum of z occurs at both the points (25,20 ) and (0,30) is ………
A5p = 2qB2p=5qCp = 2qDq = 3p
The corner points of the feasible region determined by the system of linear constraints are as shown below:
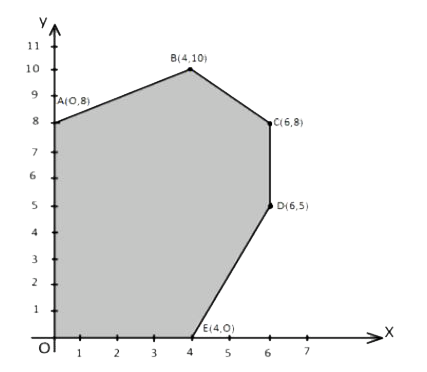
Let Z=3x−4y be the objective function. Find the maximum and minimum value of Z and also the corresponding points at which the maximum and minimum value occurs.
View SolutionSolve the following system of linear inequations: 3x−6≥0
View SolutionFor an objective function Z=ax+by, where a,b>0, the corner points of the feasible region determined by a set of constraints (linear inequalities) are (0, 20), (10, 10), (30, 30) and (0, 40). The condition on a and b such that the maximum Z occurs at both the points (30, 30) and (0, 40) is:
View SolutionThe corner points of the feasible region determined by the system of linear contraints are (0,0), (0,40),( 20,40),(60,20),(60,0). The objective function is Z=4x+3y. Compare the quantity in Column A and Column B.
View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy , where p,q>0. Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
View Solution
