Four forces act along the sides of a smoth square frma ABCD in the order A→B,B→C,C→D and D→A. If the magnetiude of the force are F1,F2,F3 and F4 respectively, find the force acting on the frame . Assume F1=1N,F2=2N,F3=3NandF4=N
Let us consider x-y coordination system . The resultant of all the forces is
→F=→F1+→F2+→F3+→F4
After bringing the tails of all the vectors to a point O and
substituting →F1=1ˆiN, →F2=2ˆjN,→F3=−3ˆiN and
→F4=−4ˆjN we have
→F=−2(ˆi+ˆj)N
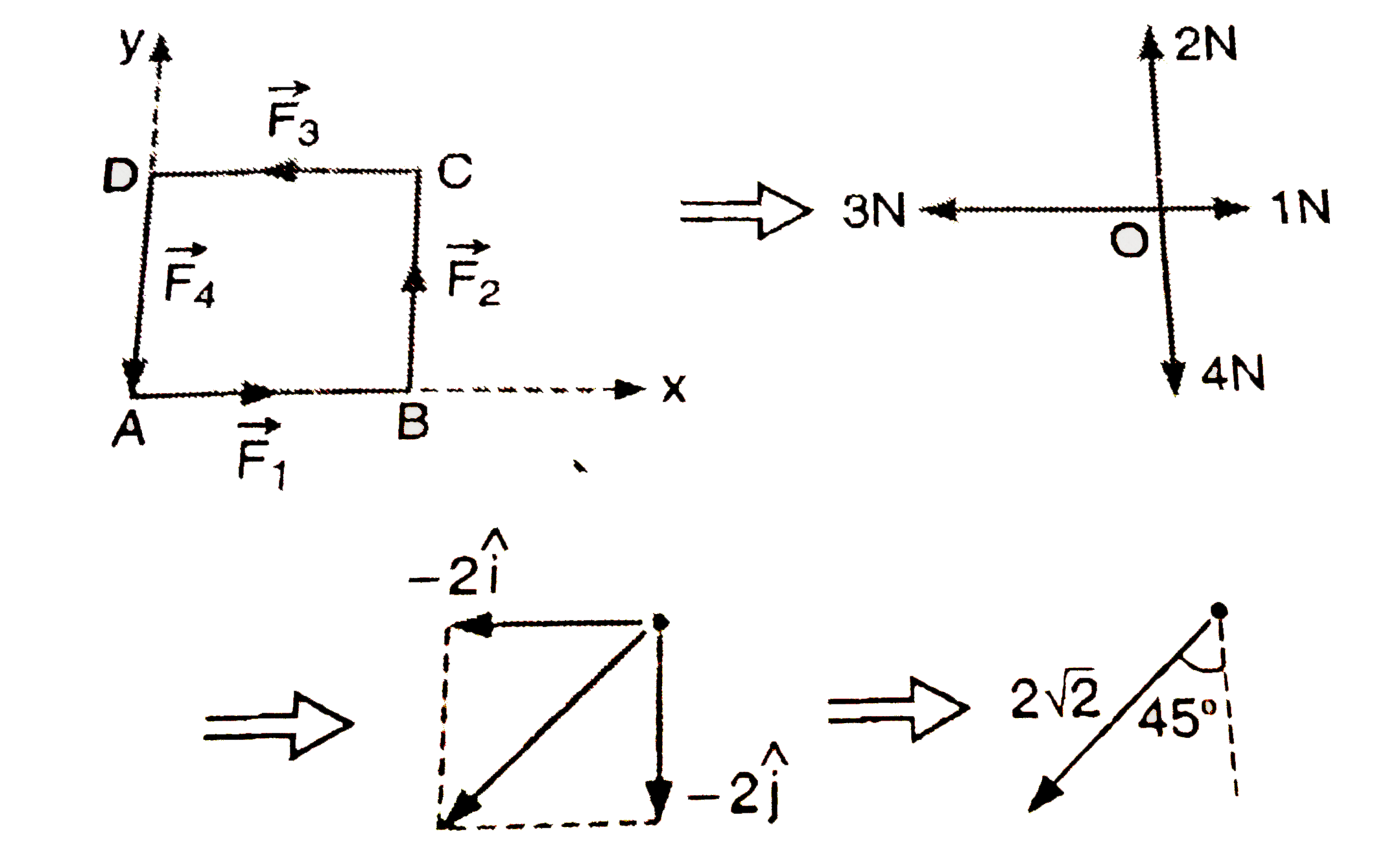
Henece the magntiude of →F, that is , ∣∣→F∣∣=2√2 is directed in 3rd quadrant , as shown in the Fig. 3.39
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Let us consider two forces F1 and F2 acting on a body of mass 2 kg as shown in the figure. F1=10N, F2=2N , what will be the acceleration?
 A4B1C2D3
A4B1C2D3 - Question 2 - Select One
Two forces −→F1and−→F2 are acting at right angles to each other , find their resultant ?
A√F21−F22B√F21+F22C√(F1+F2)DF1+F2 - Question 3 - Select One
Two forces of mangitude F1 and F2 are acting on an object.The magnitude of the net force Fnet on the object will be in the range.
AF1≤Fnet≤F2B|F1−F2|/2≤Fnet≤(F1+F2)/2C|F1−F2|≤Fnet≤F1+F2D|F1−F2|≥Fnet|F1+F2|
A smooth track in the form of a quarter-circle of radius 6 m lies in the vertical plane. A ring of weight 4(N) moves from P1 and P2 under the action of forces F1,F2 and F3. is always towards P2 under the action of forces F1,F2 and F3 Force F1 is always towards P2 and is always (20) N in maghitude, force F2 always acts hotizontally and is always (30 N) in magnitude, force F3 always acts tangentially to the track and is of magnitude (15−10s)N, where s is in metre. If the particle has speed 4m/s at P1,what will its speed be at P2?
View SolutionIn the figure, the blocks A,B and C of mass m each have accelerations a1,a2 and a3 respectively. F1 and F2 are external forces of magnitude 2mg and mg respectively.
 View Solution
View SolutionA deuteron and an α-particle are placed in an electric field.The forces acting on them are F1 and F2 and their accelerations are a1 and a2 respectively.
(i) F1=F2
(ii) F1≠F2
(iii) a1=a2
(iv) a1≠a2View SolutionIn the figure, the blocks A,B and C of mass m each have accelerations a1,a2 and a3 respectively. F1 and F2 are external forces of magnitude 2mg and mg respectively.
 View Solution
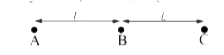
View SolutionThree particles A, B and C of mass m, m and 2m lie in a straight line as shown. The only force acting on these particles is due to the gravitational attraction towards each other. Let the magnitude of net force on them be FA,FB and FC respectively. Then,FA:FB:FC is equal to :
 View Solution
View Solution