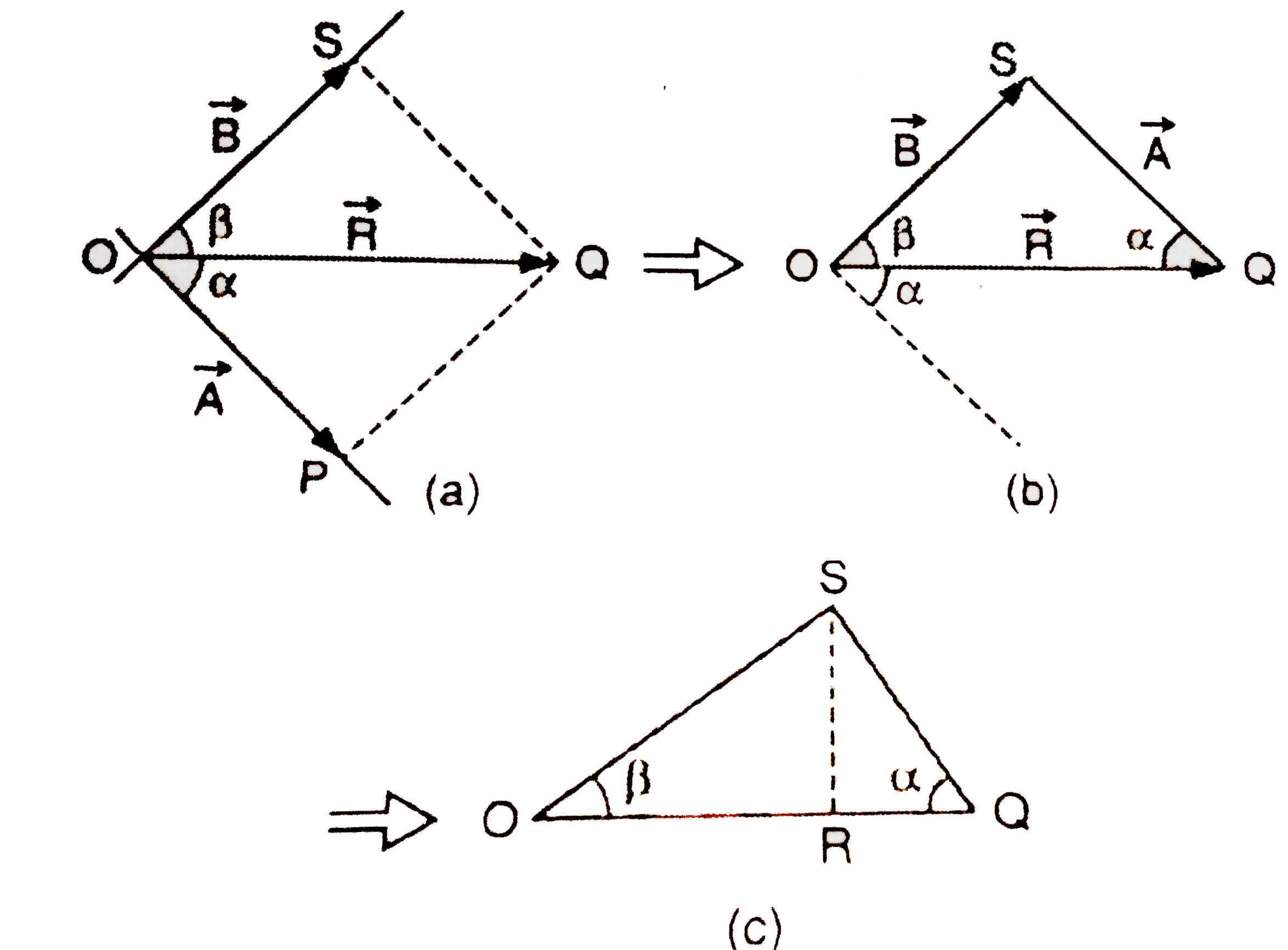
Find the components of a vector $\to R$ along two straight lines stiuated at both sides of the vector $\to R$ making angles $α$ and $β$ with it.

Video Solution

Text Solution

Verified by Experts

Since the components $\to A and \to B$ of the given
vector $\to R$ are choose in the given directions, $\to R$ is the resultant of
$\to A$ and $\to B$ , then , $\to R = \to A + \to B$ . Hence, R is repersented by the
diagonal OQ of the square $O P Q S$ where the component vectors $\to A$
and $\to B$ respresented by the adjacent sides OP and OS
respectivcely according to the parallelogram law of vectors.
Then we convert the parallelorgam OSQP to the vectors triangle
OSQ which represents the vectos $\to R, \to A and \to B$ as shown in the
Fig. 3.40 (a). By converting to a scalar triangle OSQ as shown in the Fig. 3.40 (c), we can write
$O Q = O S cos β + S Q cos α ... . (i)$
and $S R = O S sin β = S Q sin α ... ... (i i)$
Solving the Eqs. (i) and (ii), we have
$Q S = ∣ ∣ \to A ∣ ∣ = \frac{O Q sin β}{sin (α + β)} = \frac{R sin β}{sin (α + β)}$
and $O S = ∣ ∣ \to B ∣ ∣ = \frac{R sin α}{sin (α + β)}$

Alternate solution
Using Lami,s theorm, we have
$\frac{∣ ∣ \to A ∣ ∣}{sin β} = \frac{∣ ∣ \to B ∣ ∣}{sin α} = \frac{∣ ∣ \to R ∣ ∣}{sin {180^{\circ} - (α - β)}}$

This yields $∣ ∣ \to A ∣ ∣ = \frac{∣ ∣ \to R ∣ ∣ sin β}{sin (α + β)} and ∣ ∣ \to B ∣ ∣ = \frac{∣ ∣ \to R ∣ ∣ sin α}{sin (α + β)}$

Updated on:21/07/2023

The angle between two vector A and B is $θ$ . Vector R is the resultant of the two vectors. If R makes an angle $\frac{θ}{2}$ with A, then
AA=2B
B $A = \frac{B}{2}$
CA = B
DAB = 1
Find the ratio of the magnetic potential due to the magnetic dipole at two equidisatant points.One of them along a line making an angle of $30^{\circ}$ with the magnetic dipole moment vector of $60^{\circ}$ with the magnetic diopole vector.
A $2 : \sqrt{3}$
B $\sqrt{3} : 1$
C $3 : \sqrt{3}$
D $1 / \sqrt{3} : 4$