A particle is moving on a cicular path of radius 'R' . As it moves through an angular displacement $θ$ , its linear displacement will be :

Video Solution

Text Solution

Verified by Experts

The correct Answer is:In the foregoing example, find the angle between $\vec{A}$ and $\vec{B}$ .
' $θ = \cos^{- 1} {\frac{A_{x} B_{x} + A_{y} B_{y} + A_{z} B_{z}}{\sqrt{(A_{x}^{2} + A_{y}^{2} + A_{z}^{2}) (B_{x}^{2} + B_{y}^{2} + B_{z}^{2})}}}$

When the insect moves from positon to position 2, the displacement $\vec{s}$ = change in position vectors $Δ \vec{r}$ .
Since $Δ \vec{r} = {\vec{r}}_{2} - {\vec{r}}_{1}$ , the magnitude of the displacement is
$| Δ \vec{r} | = \sqrt{r_{1}^{2} + r_{2}^{2} - 2 r_{1} r_{2} \cos θ} .$

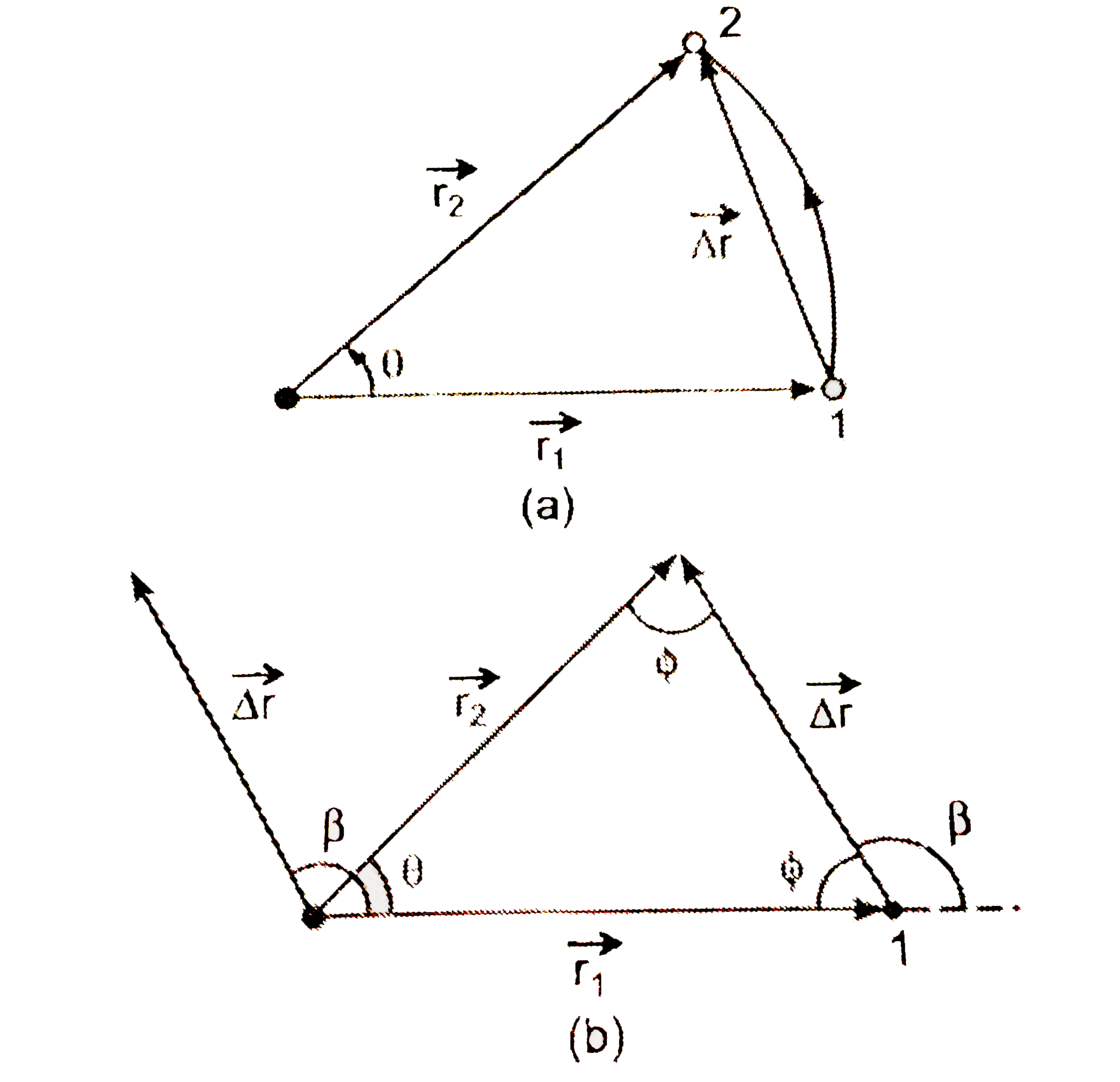
Since the insect moves in a circular path, $r_{1} = r_{2} = R$
Hence $| Δ \vec{r} | = 2 R \sin . \frac{θ}{2}$ . The direction of $Δ \vec{r}$ is given as
$β = \frac{π}{2} + \frac{θ}{2}$ , as shown in the Fig.3.42 .

|

Updated on:21/07/2023

Class 11 PHYSICS VECTOR

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle is moving uniformly in a circular path of radius r. When it moves through an angular displacement $θ$ , then the magnitude of the corresponding linear displacement will be
A2 r cos $(\frac{θ}{2})$
B2 r cot $(\frac{θ}{2})$
C2 r tan $(\frac{θ}{2})$
D2 r sin $(\frac{θ}{2})$
Question 2 - Select One
A particle is moving in a circular path of radius 'r'. The displacement after half a circle would be
A0
B $π r$ ,
C $2 r$
D $2 π r$
Question 3 - Select One
A particle moves through angular displacement $θ$ on a circular path of radius' r'. The linear displacement will be:
A $2 r sin (\frac{θ}{2})$
B $2 r cos (\frac{θ}{2})$
C $2 r tan (\frac{θ}{2})$
D $2 r cot (\frac{θ}{2})$

GRB PUBLICATION-VECTORS-PASSAGE -3

Home
Ask Doubt
Profile