A particle moves along ellipatical path gives by
Calculate (i) radial component of acceleration (→ar)
(ii) trasverse component of acceleration (→aθ).
The correct Answer is:→ar=−ω→r and →aθ=0
Step by step video, text & image solution for A particle moves along ellipatical path gives by Calculate (i) radial component of acceleration (veca_(r)) (ii) trasverse component of acceleration (veca_(theta)). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - GRB PUBLICATIONCHAPTER - VECTORSEXERCISE - OBJECTIVE QUESTIONS120videos
VECTORS
- BOOK - GRB PUBLICATIONCHAPTER - VECTORSEXERCISE - MORE THAN ONE CHOICE IS CORRECT15videos
VECTORS
- BOOK - GRB PUBLICATIONCHAPTER - VECTORSEXERCISE - PASSAGE -33videos
VECTORS
- BOOK - GRB PUBLICATIONCHAPTER - UNITS AND DIMENSIONSEXERCISE - Link Compression6videos
UNITS AND DIMENSIONS
Similar Questions
A particle moves in a plane along an elliptic path given by x2a2+y2b2=1 At point (0, b), the x-component of velocity is u. The y-component of acceleration at this point is-
View SolutionA particle moves along a path y=ax2 (where a is constant) in such a way that x-component of its velocity (ux) remains constant. The acceleration of the particle is
View Solution
Knowledge Check
- Question 1 - Select One
A particle is moving along an elliptical path with constant speed. As it moves from A to B, magnitude of its acceleration :
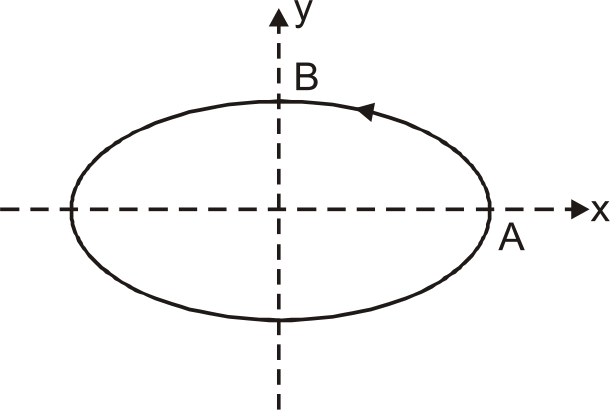 AContinuously increasesBcontinuously decreasesCRemains constantDfirst increases and then decreases
AContinuously increasesBcontinuously decreasesCRemains constantDfirst increases and then decreases - Question 2 - Select One
A particle is moving along an elliptical path with a constant speed. As it moves from A to B, magnitude of its acceleration:
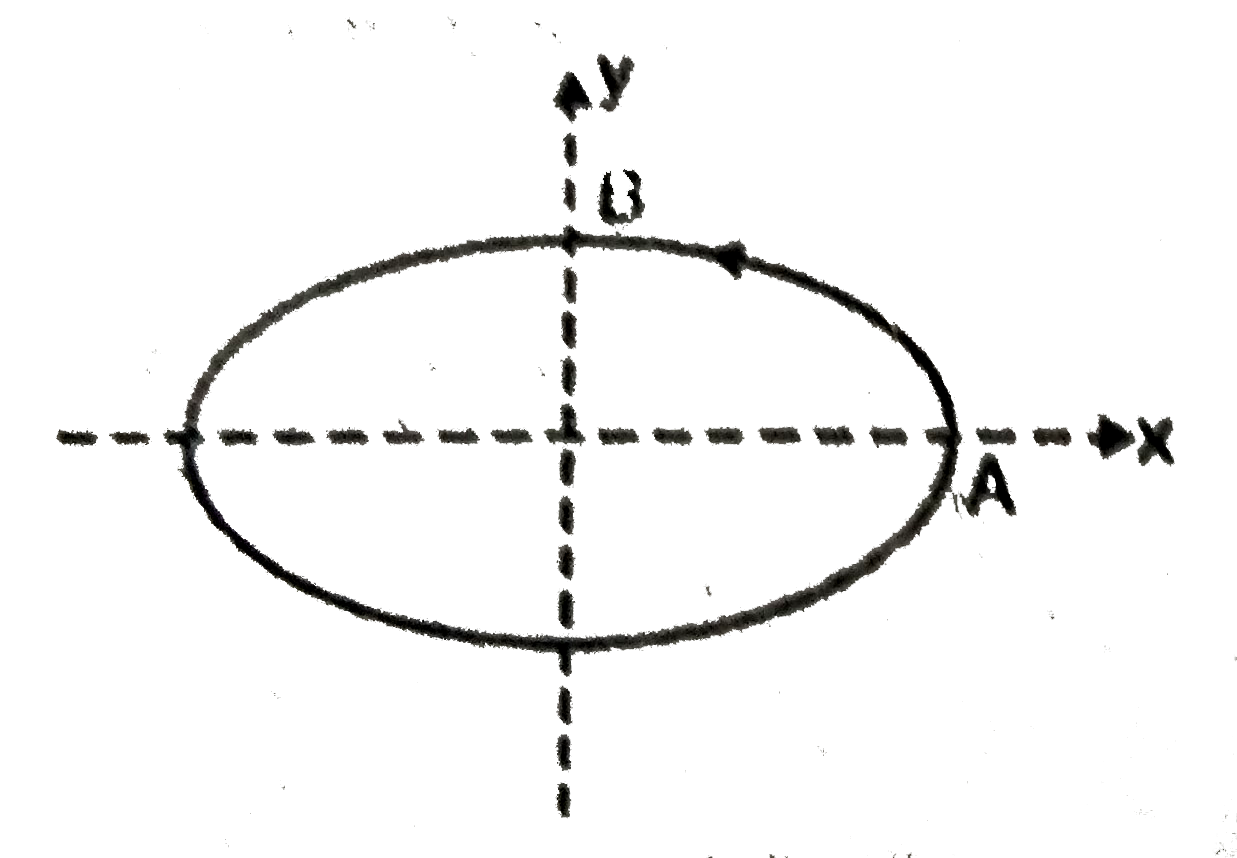 AContinuously increasesBcontinuoulsy decreasesCremains constantDfirst increases and then decreases
AContinuously increasesBcontinuoulsy decreasesCremains constantDfirst increases and then decreases - Question 3 - Select One
A particle moves along the parabolic path x=y2+2y+2 in such a way that Y-component of velocity vector remains 5ms−1 during the motion. The magnitude of the acceleration of the particle is
A50ms−2B100ms−2C10(√2)ms−2D0.1ms−2
(a) A point moving in a circle of radius R has a tangential component of acceleration that is always n times the normal component of acceleration (radial acceleration). At a certain instant speed of particle is v0. What is its speed after completing one revolution?
(b) The tangential acceleration of a particle moving in xy plane is given by at=a0cosθ. Where a0 is a positive constant and q is the angle that the velocity vector makes with the positive direction of X axis. Assuming the speed of the particle to be zero at x=0, find the dependence of its speed on its x co-ordinate.View SolutionA particle moves along a semicircular path of radius R in time t with constant speed. For the particle calculate
View SolutionIf a body moves along circular path of constant radius, then the magnitude of its acceleration will be
View SolutionA particle is performing non UCM, the acceleration of the particle is →aR=→ar+→aT , where →ar is radial component of acceleration. If →ar=0, the motion of the particle is
View SolutionA particle is moving along a circular path of radius of R such that radial acceleration of particle is proportional to t2 then
View Solution

