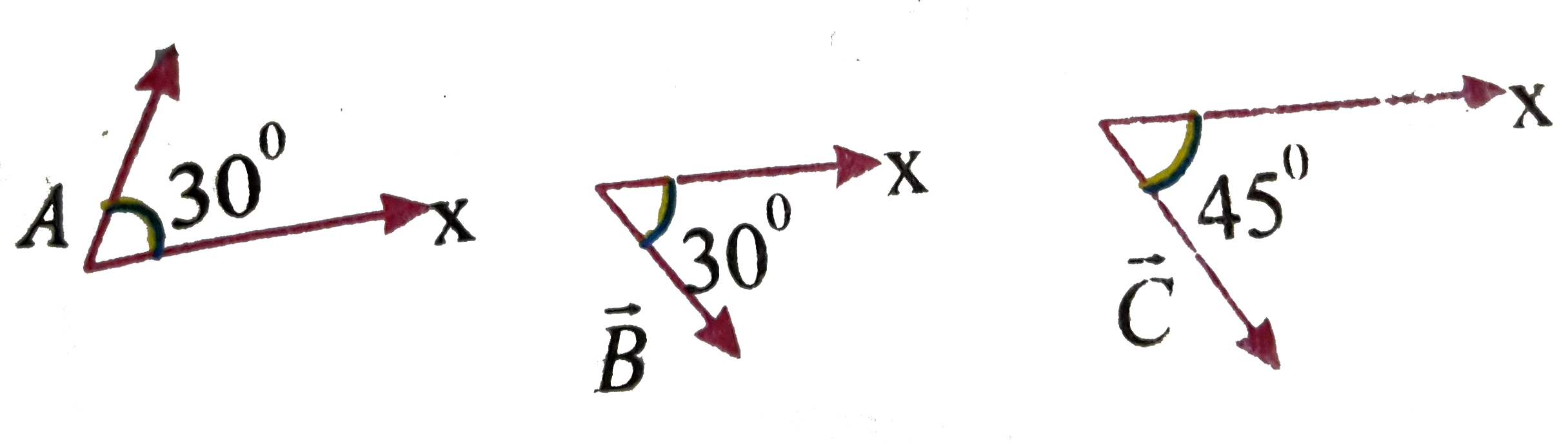Consider three vectors →A,→Band→C having magnitudes 4, 5, and 3. These vectors are of similar nature, e.g. these could be there displacement. Apply your answer understanding of vectors algebra to match Column-I with Column-II.

Video Solution
Text Solution
The correct Answer is:a→r;b→p;c→s;d→q
∣∣→A∣∣=4,∣∣→B∣∣=5,∣∣→C∣∣=3
|
Topper's Solved these Questions
- VECTORSBOOK - GRB PUBLICATIONCHAPTER - VECTORSEXERCISE - INTERGER ANSWER
9 Videos
- VECTORSBOOK - GRB PUBLICATIONCHAPTER - VECTORSEXERCISE - PASSAGE -1
3 Videos
- VECTORSBOOK - GRB PUBLICATIONCHAPTER - VECTORSEXERCISE - ASSERTION- REASON
1 Video
- UNITS AND DIMENSIONSBOOK - GRB PUBLICATIONCHAPTER - UNITS AND DIMENSIONSEXERCISE - Link Compression
6 Videos
Similar Questions
Knowledge Check
Two vectors →Aand→B lie in plane, another vector →C lies outside this plane, then the resultant of these three vectors i.e., →A+→B+→C
ACan be zeroBCannot be zeroCLies in the plane containing →A+→BDLies in the plane containing →CA magnitude of vector →A,→B and →C are respectively 12,5 and 13 units and →A+→B=→C then the angle between →A and →B is
A0BπCπ/2Dπ/4The magnitudes of vectors →A,→Band→C are 3,4 and 5 units respectively. If →A+→B=→C, the angle between →A and →B is
Aπ2Bcos−1(0.6)Ctan−1(75)Dπ4
Find a vector which is parallel to vector →A=4ˆi−3ˆj
and have the same magnitude as vector →B=8ˆi+6ˆj .
View SolutionTheree coplanar vectors →A,→B and →C have magnitudes 4.3 and 2 respectively. If the angle between any two vectors is 120∘ then which of the following vector may be equal to 3→A4+→B3+→C2

View Solution→A,→B and →C are three orthogonal vectors with magnitudes 3, 4 and 12 respectively. The value of ∣∣→A−→B+→C∣∣ will be :-
View SolutionLet →a,→b and →c be three vectors having magnitudes 1,1 and 2 resectively. If →a×(→a×→c)+→b=→0 then the acute angel between →a and →c is
View SolutionLet →a,→band→c be the three vectors having magnitudes, 1,5 and 3, respectively, such that the angle between →aand→bisθand→a×(→a×→b)=→c. Then tanθ is equal to
View Solution