In a hydrogen atom, the transition takes place from n=3 to n=2 . If Rydberg constant is 1.097×107m−10. The wavelength of the emiited radiation is
365RH
5RH36
34RH
43RH
The correct Answer is:A
1λ=R11z2[1n21−1n22]
1λ=R11×(1)2[14−19]
1λ=R11[536]
=λ=365R11
Topper's Solved these Questions
Similar Questions
In a hydrogen atom, a transition takes place from n = 3 to n = 2 orbit. Calculate the wavelength of the emitted photon. Will the photon be visible ? To which spectral series will this photon belong? Given R=1.097×107m−1
View SolutionIn a hydrogen atom, a transition takes place from n = 3 to n = 2 orbit. Calculate the wavelength of the emitted photon. Will the photon be visible ? To which spectral series will this photon belong? Given R=1.097×107m−1
View Solution
Knowledge Check
In a hydrogen atom, the transition takes place from n = 3 to n = 2 . If Rydberg constant is 1.097×107m−1 , the wavelength of the emitted radiation is
A365RHB5RH36C34RHD43RHIn hydrogen atom, the transition takes place from n=3 to n=2. If Rydberg's constant is 1.09×10 per metre, the wavelength of the limit emitted is
A6606ÅB4861ÅC4340ÅD4101ÅThe wavelength of the radiation emitted by a hydrogen atom in the electronic transition from n=3 to n=2 is λ. For the same transition in the singly ionized helium, the wavelength of the emitted radiation is
Aλ/4Bλ/2C2λD4λ
Energy level diagram of a hydrogen atom is shown below :
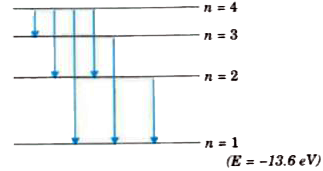
(i)If a transition takes place from n=3 to n=2 orbit, calculate the wavelength of the radiation emitted. Identify the spectral series to which it belongs.
(ii)Which transition results in emission of radiation of maximum wavelength ?
View SolutionThe Rydberg constant for hydrogen is 1.097×107m−1. Calculate the short and long wavelength limits of Lyman series.
View SolutionWhat is the energy difference and the frequancy and the wavelength of light emitted when the electron in a hydrogen atom undergoes transition from the energy level n=4 to the energy n=3 given that the value of Rydberg constant is 1.0974×107m−1?
View SolutionAn electron makes a transition from orbit n=4 to the orbit n=2 of a hydrogen atom. The wave length of the emitted radiations (R= Rydberg's constant) will be
View SolutionTaking Rydberg's constant RH=1.097×107m first and second wavelength of Balmer series in hydrogen spectrum is
View Solution
