What is the total no of planes of symmetry in a cube ?
To determine the total number of planes of symmetry in a cube, we can follow these steps:
1. Understanding Planes of Symmetry: A plane of symmetry is an imaginary plane that divides an object into two equal halves that are mirror images of each other.
2. Identifying Planes in a Cube: A cube has several planes that can serve as planes of symmetry. We can categorize them based on their orientation:
- Planes parallel to the faces of the cube:
- There are three planes that cut through the center of the cube, parallel to each pair of opposite faces. Each of these planes divides the cube into two equal halves.
- These planes are:
- One plane parallel to the front and back faces.
- One plane parallel to the left and right faces.
- One plane parallel to the top and bottom faces.
3. Identifying Diagonal Planes: In addition to the planes parallel to the faces, there are also diagonal planes:
- Diagonal planes:
- There are six diagonal planes. Each diagonal plane cuts through the vertices of the cube and divides it into two symmetrical halves.
- These planes can be visualized as:
- One plane that connects the diagonally opposite edges of the cube.
- This can be done for each pair of opposite edges, leading to six unique diagonal planes.
4. Counting the Total Planes of Symmetry:
- From the analysis, we have:
- 3 planes parallel to the faces.
- 6 diagonal planes.
- Therefore, the total number of planes of symmetry in a cube is:
3 (face planes)+6 (diagonal planes)=9 planes of symmetry.
Final Answer:
The total number of planes of symmetry in a cube is 9.
---
- Planes parallel to the faces of the cube:
- There are three planes that cut through the center of the cube, parallel to each pair of opposite faces. Each of these planes divides the cube into two equal halves.
- These planes are:
- One plane parallel to the front and back faces.
- One plane parallel to the left and right faces.
- One plane parallel to the top and bottom faces.
- Diagonal planes:
- There are six diagonal planes. Each diagonal plane cuts through the vertices of the cube and divides it into two symmetrical halves.
- These planes can be visualized as:
- One plane that connects the diagonally opposite edges of the cube.
- This can be done for each pair of opposite edges, leading to six unique diagonal planes.
- From the analysis, we have:
- 3 planes parallel to the faces.
- 6 diagonal planes.
- Therefore, the total number of planes of symmetry in a cube is:
3 (face planes)+6 (diagonal planes)=9 planes of symmetry.
The total number of planes of symmetry in a cube is 9.
Topper's Solved these Questions
- BOOK - DINESH PUBLICATIONCHAPTER - SOLID STATEEXERCISE - Matrix4videos
SOLID STATE
- BOOK - DINESH PUBLICATIONCHAPTER - SOLID STATEEXERCISE - Brain storming10videos
SOLID STATE
- BOOK - DINESH PUBLICATIONCHAPTER - SOLID STATEEXERCISE - A.R27videos
SOLID STATE
- BOOK - DINESH PUBLICATIONCHAPTER - REDOX REACTIONSEXERCISE - Ultimate Preparation9videos
REDOX REACTIONS
- BOOK - DINESH PUBLICATIONCHAPTER - SOLUTIONS EXERCISE - ULTIMATE PREPARATORY PACKAGE10videos
SOLUTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The total number of elements of symmetry in a cubic crystal is
A9B23C10D14 - Question 2 - Select One
The total number of elements of symmetry in a cubic crystal is
A9B23C9Dnone of these - Question 3 - Select One
Which species have a plane of symmetry?
A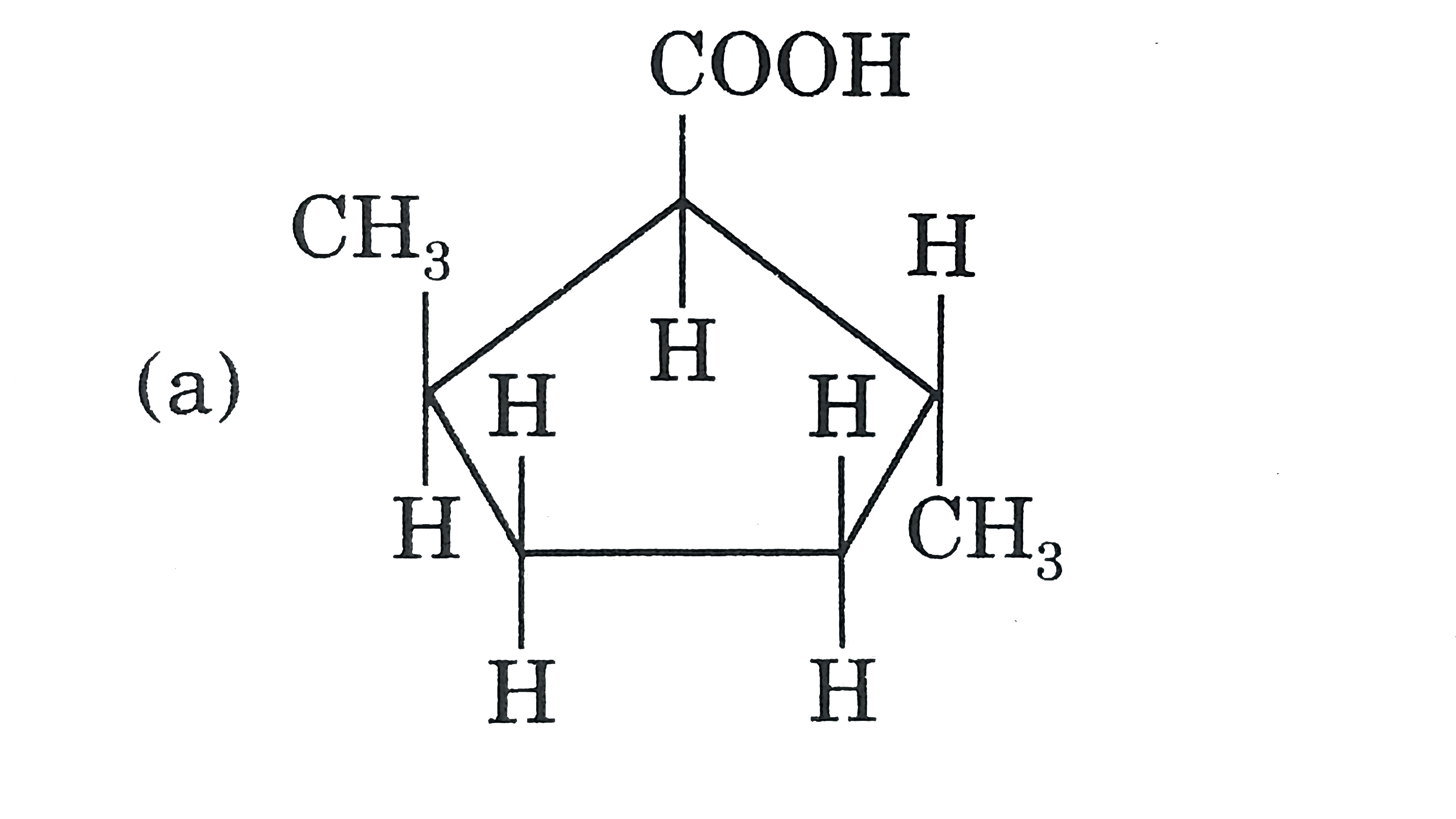 B
B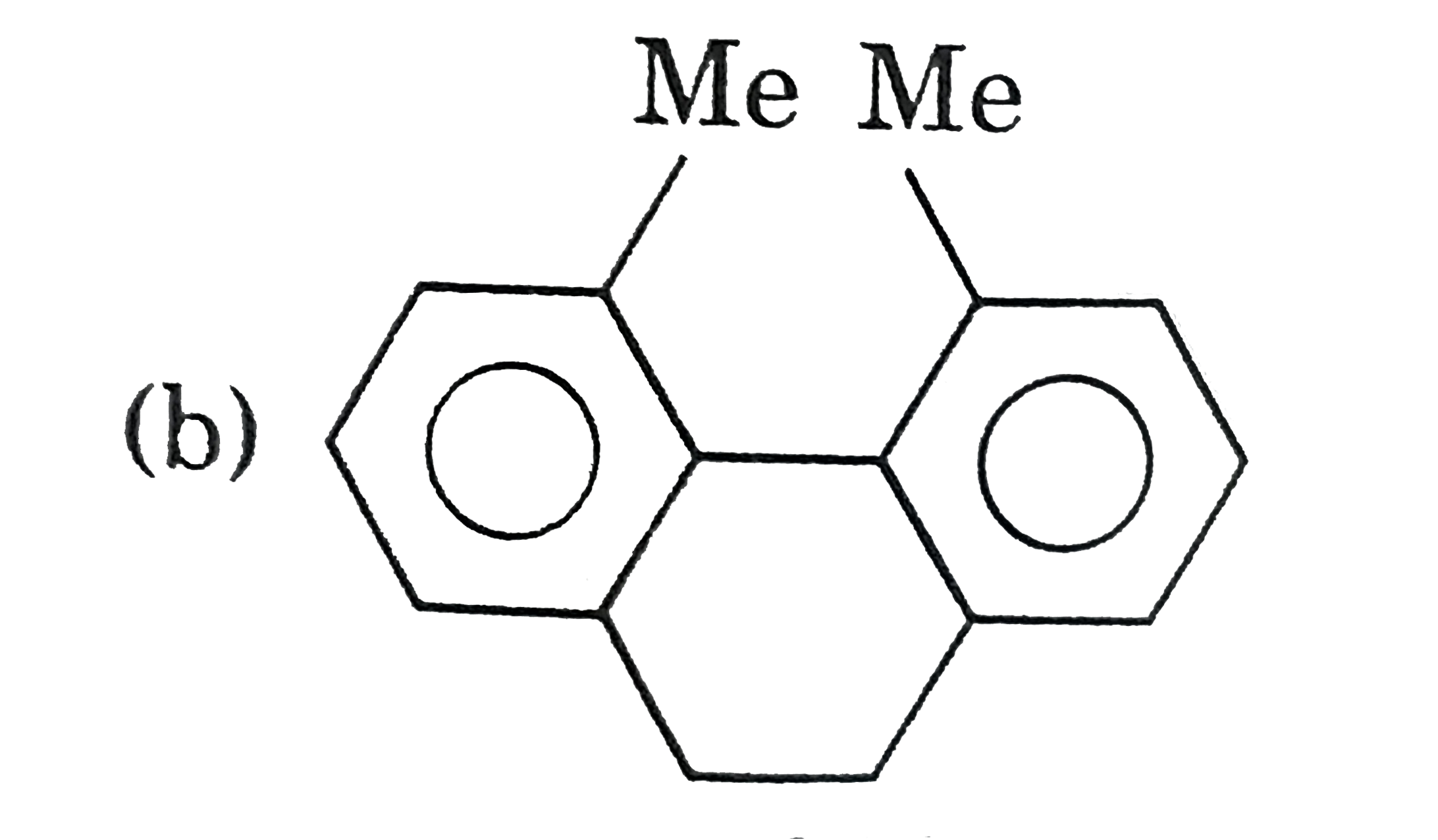 C
C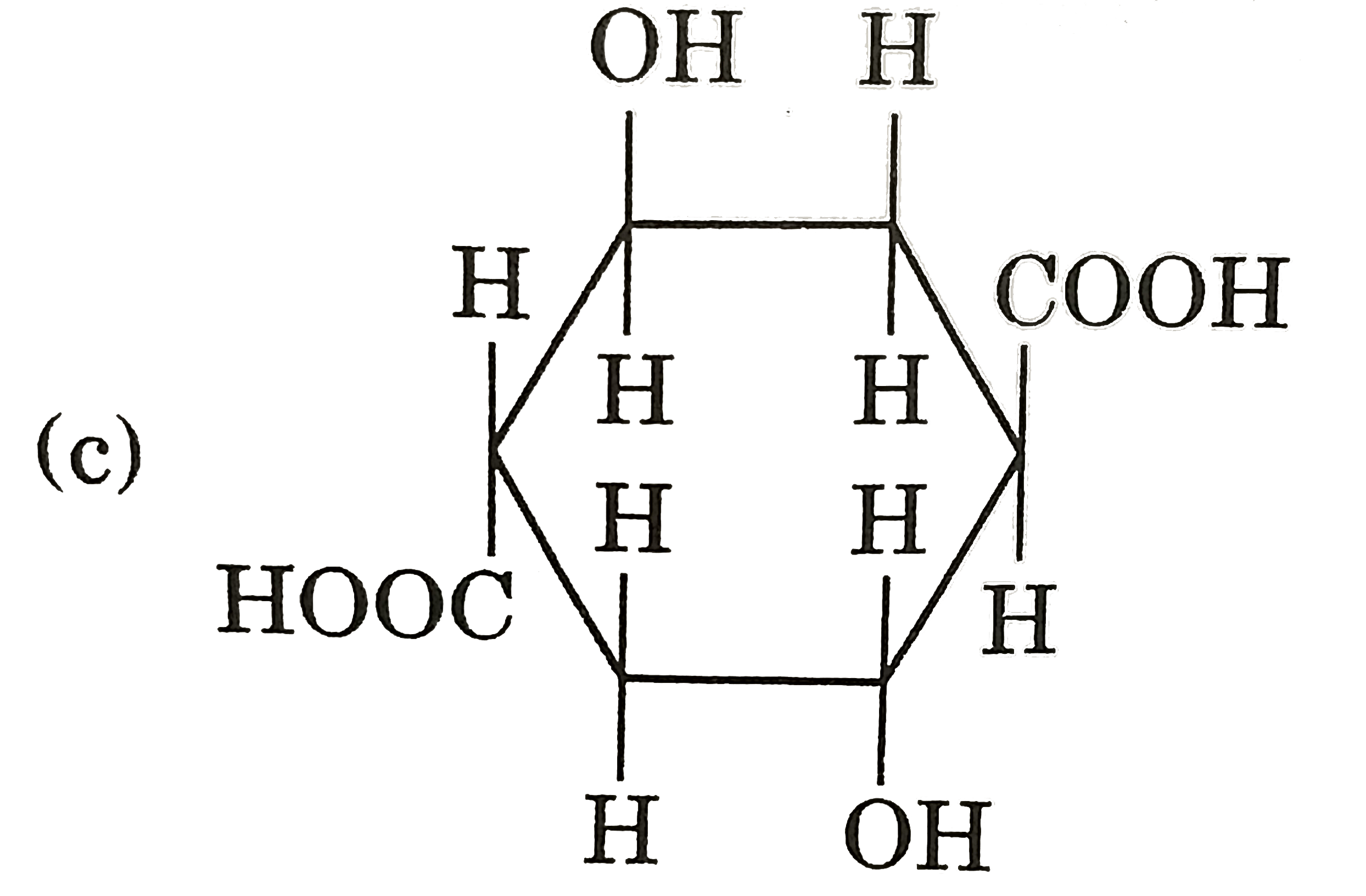 D
D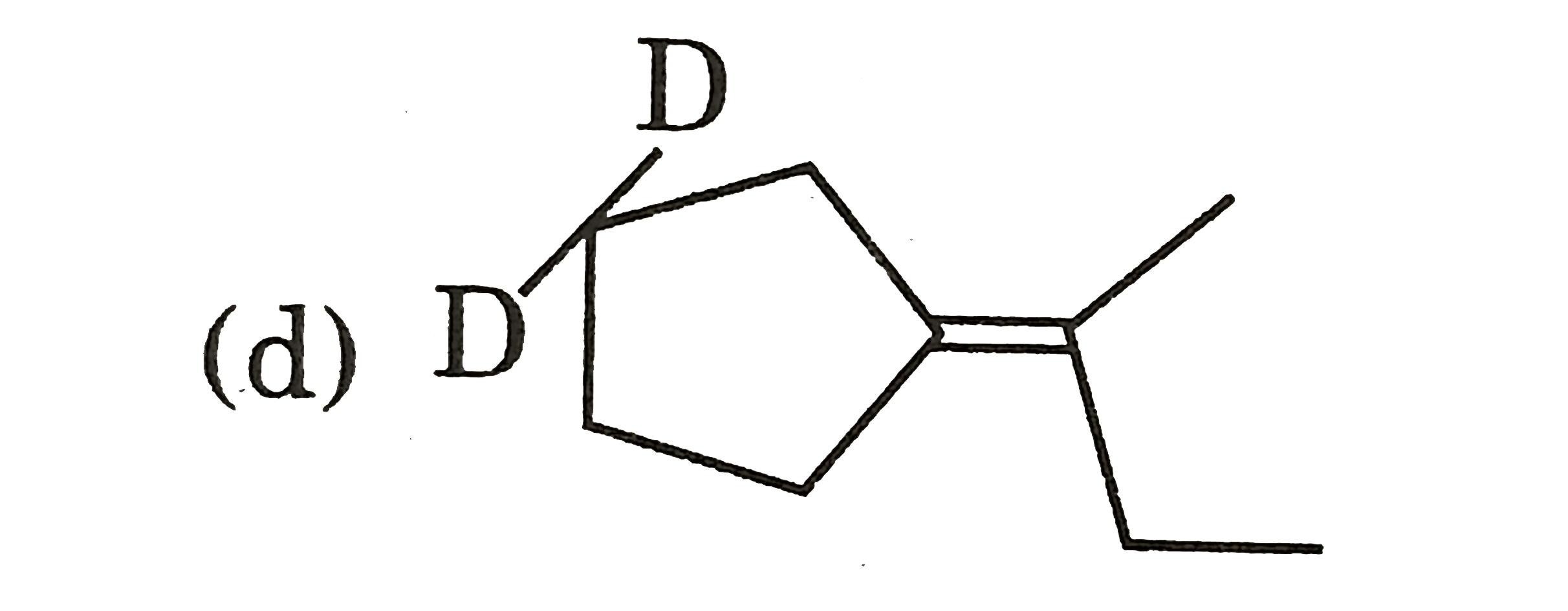
Plane OF Symmetry
View SolutionWhat is the number of lines of symmetry and order of rotational symmetry of a regular hexagon?
View SolutionThe number of planes of symmetry in SbF5 is _____ .
View SolutionIn which of the following compounds plane of symmetry and center of symmetry both are present?
View SolutionIn which of the following compounds plane of symmetry and center of symmetry both are present?
View Solution

