If the diameter through any point P of a parabola meets any chord in A and the tangent at the end of the chord meets the diameter in B and C, then prove that PA2=PB.PC
Step by step video & image solution for If the diameter through any point P of a parabola meets any chord in A and the tangent at the end of the chord meets the diameter in B and C, then prove that PA^2=PB.PC by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Tangents at the end of focal chord are perpendicular to each other and meet at directrix
View SolutionProve that the tangents at the extremities of any chord make equal angles with the chord.
View SolutionProve that the tangents at the extremities of any chord make equal angles with the chord.
View SolutionThrough a point A on a circle, a chord AP is drawn & on the tangent at A a point T is taken such that AT=AP. If TP produced meet the diameter through A at Q, prove that the limiting value of AQ when P moves upto A is double the diameter of the circle.
View SolutionThe tangents at the end points of any chord through (1,0) to the parabola y2+4x=8 intersect
View SolutionThe tangents at the end points of any chord through (1,0) to the parabola y2+4x=8 intersect
View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :
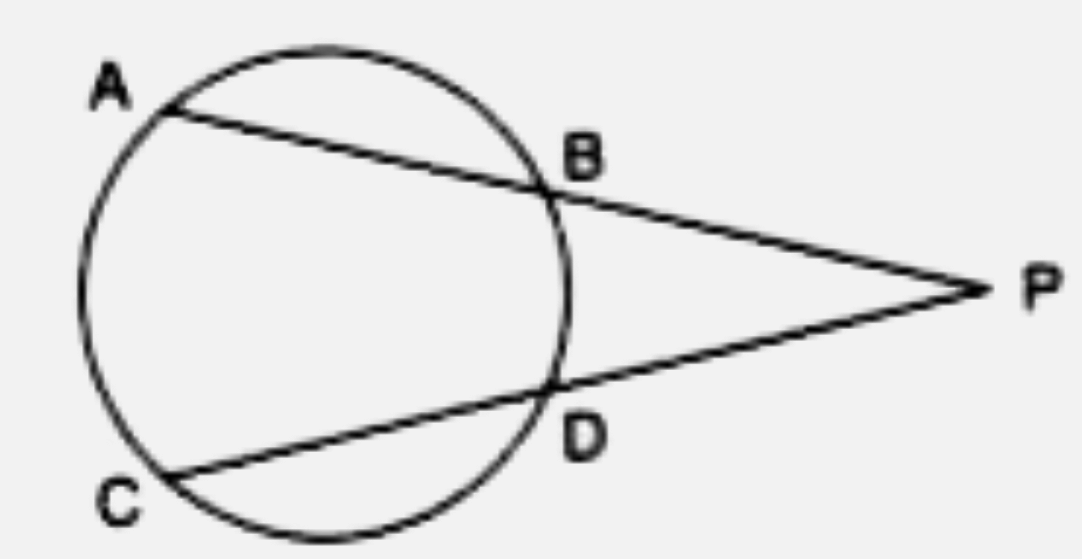
PA=PC.
View SolutionThe tangent at any point P of a circle x2+y2=a2 meets the tangent at a fixed point A(a,0) in T and T is joined to B, the other end of the diameter through A, prove that the locus of the intersection of AP and BT is an ellipse whose eccentricity is 1√2
View SolutionIf a chord of the parabola y2=4ax touches the parabola y2=4bx, then show that the tangent at the extremities of the chord meet on the parabola b2y2=4a2x.
View SolutionLet λx−y+7=0 is any chord of the parabola x2=28ymeeting at A and B and the tangents drawn to the parabola at A,B meet at C , then locus of circumcentre of ΔABC is
View Solution
