A 0.50 kg object moves in a horizontal circular track of radius of 2.5 m. An external force of 3.0 N, always tangent to the track, causes the object to speed up as it goes around. The work done by the external force as the object makes one revolution is :
24 J
47 J
59 J
94 J
The correct Answer is:B
To find the work done by the external force as the object makes one revolution, we can follow these steps:
Step 1: Understand the Work Done Formula
The work done (W) by a force is given by the formula:
W=F⋅d⋅cos(θ)
where:
- F is the magnitude of the force,
- d is the displacement,
- θ is the angle between the force and the direction of displacement.
Step 2: Identify the Given Values
From the problem:
- Mass of the object, m=0.50kg (not directly needed for work calculation),
- Radius of the circular track, r=2.5m,
- External force, F=3.0N.
Step 3: Calculate the Displacement for One Revolution
The displacement d for one complete revolution around a circular track is the circumference of the circle, given by:
d=2πr
Substituting the value of r:
d=2π(2.5)
Step 4: Calculate the Circumference
Now, calculate the circumference:
d=2×3.14×2.5
d=15.7m
Step 5: Determine the Angle
Since the force is always tangent to the track, the angle θ between the force and the displacement is 0∘. Therefore, cos(0∘)=1.
Step 6: Calculate the Work Done
Now, substitute the values into the work done formula:
W=F⋅d⋅cos(θ)
W=3.0N⋅15.7m⋅1
W=47.1J
Conclusion
The work done by the external force as the object makes one revolution is approximately 47.1J.
---
The work done (W) by a force is given by the formula:
W=F⋅d⋅cos(θ)
where:
- F is the magnitude of the force,
- d is the displacement,
- θ is the angle between the force and the direction of displacement.
From the problem:
- Mass of the object, m=0.50kg (not directly needed for work calculation),
- Radius of the circular track, r=2.5m,
- External force, F=3.0N.
The displacement d for one complete revolution around a circular track is the circumference of the circle, given by:
d=2πr
Substituting the value of r:
d=2π(2.5)
Now, calculate the circumference:
d=2×3.14×2.5
d=15.7m
Since the force is always tangent to the track, the angle θ between the force and the displacement is 0∘. Therefore, cos(0∘)=1.
Now, substitute the values into the work done formula:
W=F⋅d⋅cos(θ)
W=3.0N⋅15.7m⋅1
W=47.1J
The work done by the external force as the object makes one revolution is approximately 47.1J.
Similar Questions
The force acting on an object varies with the distance travelled by the object as shown in the figure. Find the work done by the force in moving the object from x=0m to x=14m.
 .
.
View SolutionA horizontal force of 10 N displaces a 5kg object through a distance of 2m in the direction of force. The work done by the force will be ________.
View Solution
Knowledge Check
An object of mass 50 kg is moving in a horizontal circle of radius 8 m . If the centripetal force is 40 N, then the kinetic energy of an object will be
A320 jB260 jC220 jD160 jA force increases the speed of a 1.0 kg object from 4 m/s to 8m/s . The work done by the force will be ____.
A8JB32JC24JD16JA force F acting on an object varies with distance x
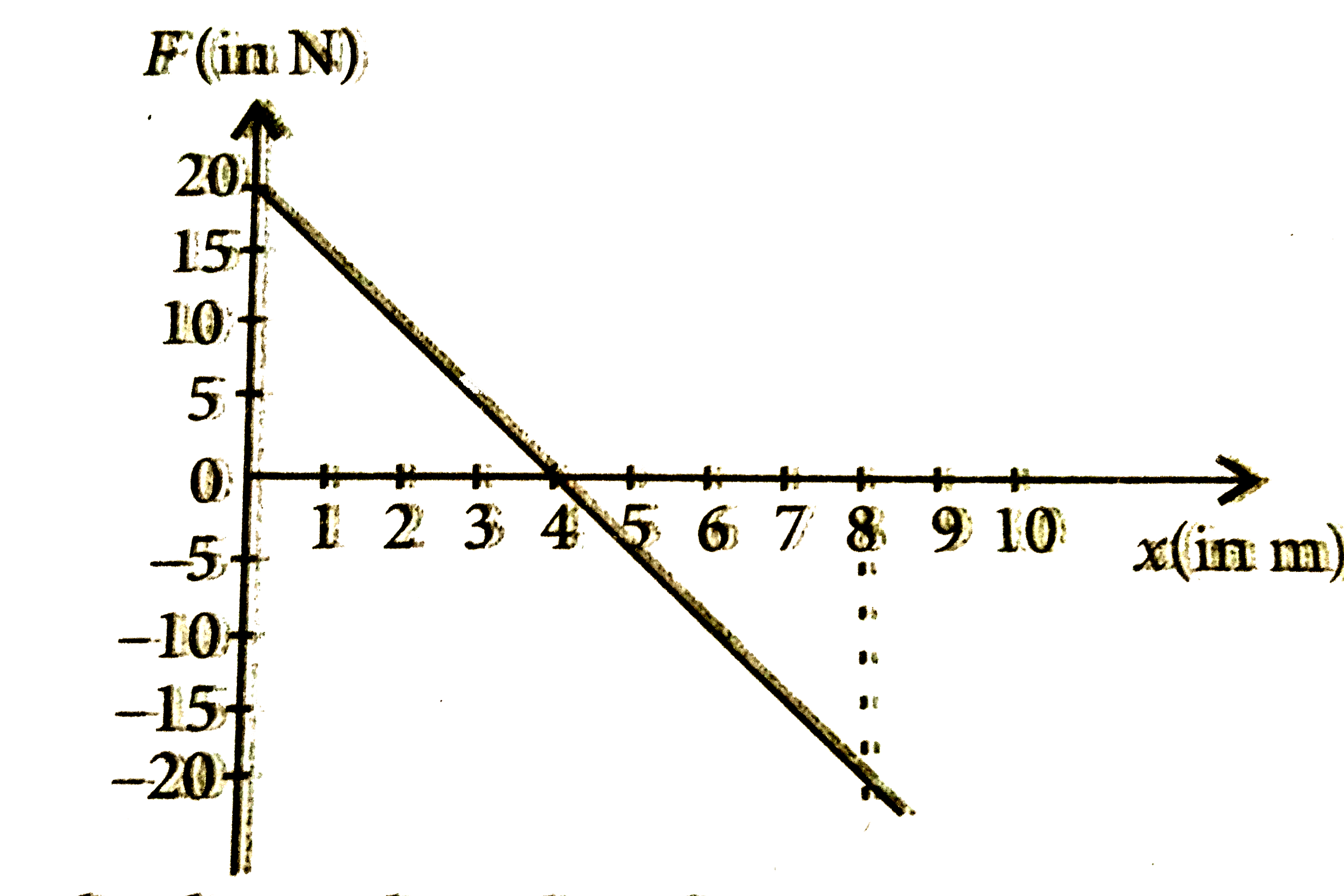
The work done by the force in moving the object from x=0 to x=8 m isAzeroB80 JC−40JD40J
A force increases the speed of a 1.0 kg object from 4 m/s to 8 m/s. The work done by the force will be __________.
View SolutionAn object of mass m moves with constant speed in a circular path of radius r under the action of a force of constant magnitude F. the kinetic energy of object is
View SolutionA body of mass 1kg is moving with a uniform speed of 1m/s in a circular path of radius 1m. The external force acting on the body is
View SolutionA force of 10N is acting on an object. The object is displaced through 5m in the directino of force. Then the work done is:
View SolutionA force F acting on an object varies with distance x as shown in the figure. The work done by the force in moving the object from x=0 to x = 20 m is

View Solution
