For a block of mass m to slide without friction up the rise of height h shown, it must have a minimum initial speed of:
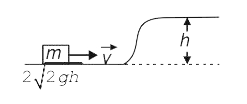
1/2√gh
√gh/2
√2gh
2√m2gh
The correct Answer is:C
Applying energy conservation , 12mv2=mgh⇒v=√2gh.
Similar Questions
A small body of mass m slide without friction from the top of a hemispherical cup of radius r as shown in figure. If leaves the surface to the cup at vertial distance h below the highest point then
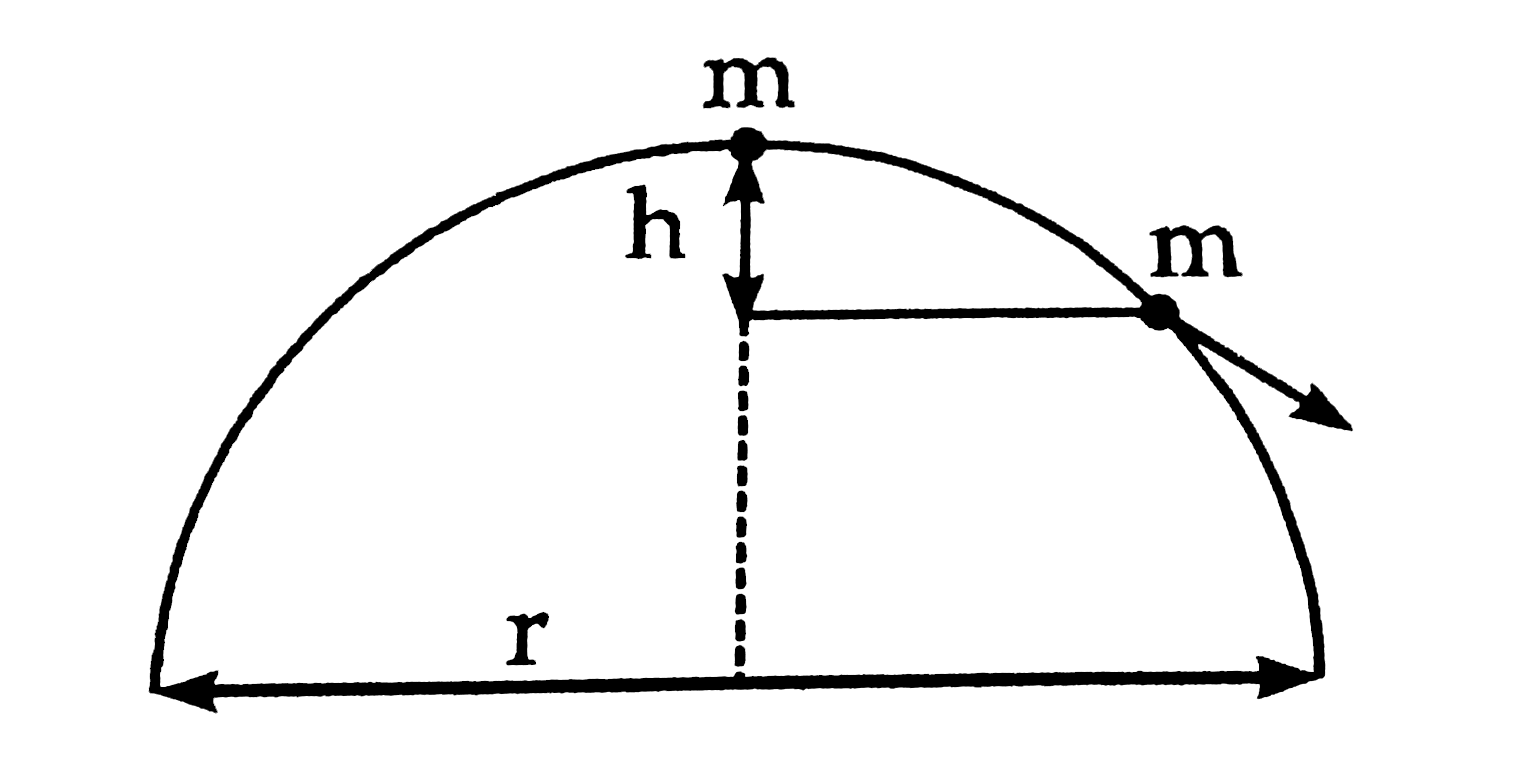 View Solution
View SolutionThe inclined surfaces of two movable wedges of the same mass M are smoothly conjugated with the horizontal plane as shown in figure. A.small block of mass m slides down the left wedge from a height h. To what maximum, height will the block rises on the right wedge.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m sliding down an inclined at constant speed is initial at a height h shown the ground as shown in the figure above . The coefficient of kinetic friction between the mass and the inclined is μ . If the mass constinues to slide down the inclined at a constant speed how much energy is displaced by friction by the time the mass reaches the bottom of the incline?
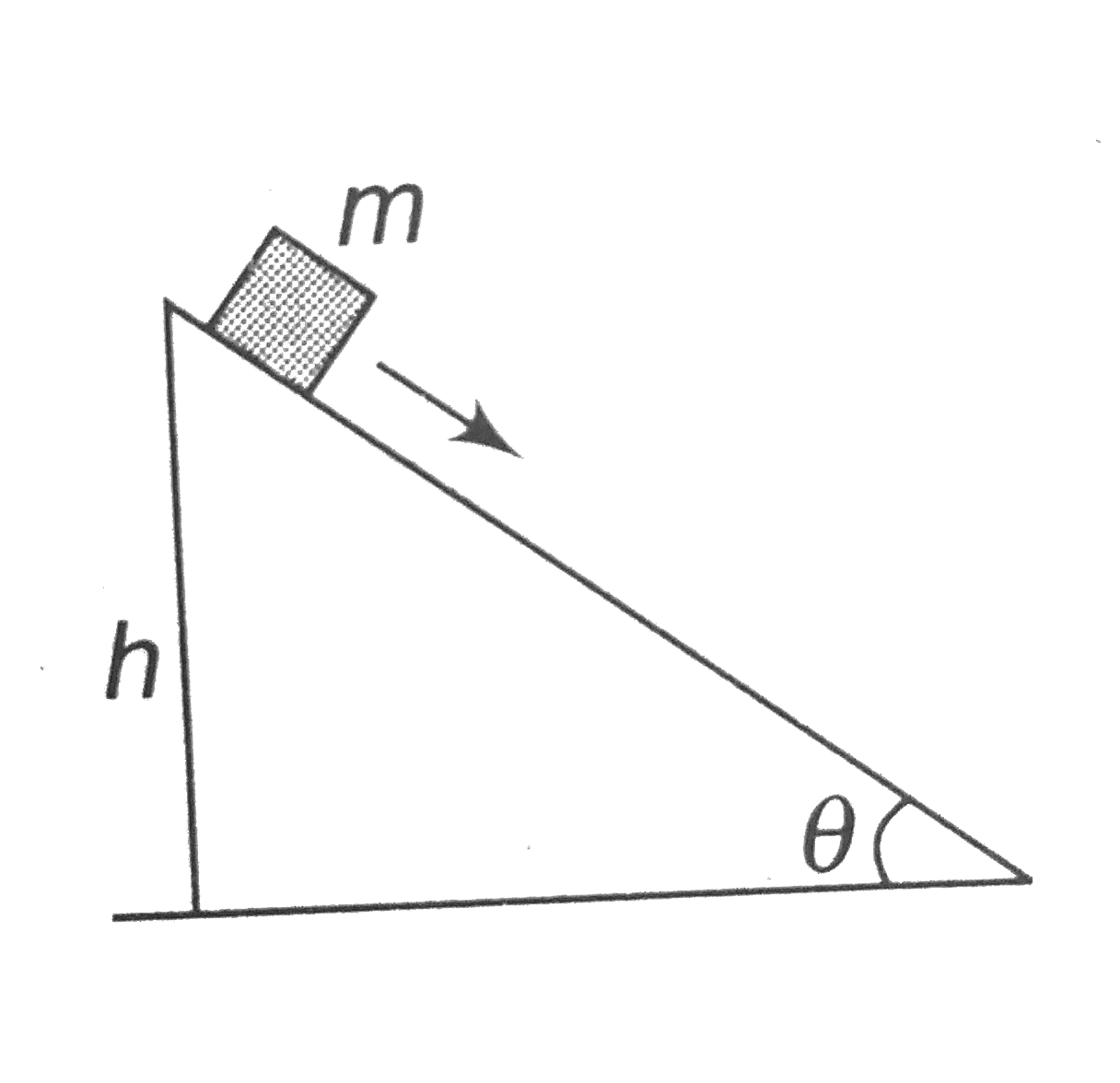 Amgh/θBmghCμmgh/sinθDmghsinθ
Amgh/θBmghCμmgh/sinθDmghsinθ - Question 2 - Select One
A man wants to slide down a block of mass m which is kept on a fixed inclined plane of inclination 30∘ as shown in the figure .Initially the block is not sliding .
To just start sliding the man pushed the block down the inclined with a force F. Now , the block starts accelerating. To move it downwards with conatant speed the man starts pulling the block with same force. Surface are such that ratio of maximum static friction to kinetic friction is 2 Now, answer the following questions.

What minimum force is required to move it up the incline with constant speed?A23mgBmg2C7mg6D5mg6 - Question 3 - Select One
Two blocks of mass 2m and m slide down the slope AB having same friction coefficient Then:
 Athe heavier mass reaches the bottom in a shorter timeBboth the masses have the same kinetic energy on arriving at BCthe heavier mass has twice the momentum than that of the other when reaching BDthe lighter mass reaches the bottom in a shorter time
Athe heavier mass reaches the bottom in a shorter timeBboth the masses have the same kinetic energy on arriving at BCthe heavier mass has twice the momentum than that of the other when reaching BDthe lighter mass reaches the bottom in a shorter time
A bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is
 View Solution
View SolutionA cube of mass m and height H slides with a speed v. It strikes the obstacle of height h=(H4). Find the speed of the CM of the cube just after the collision.
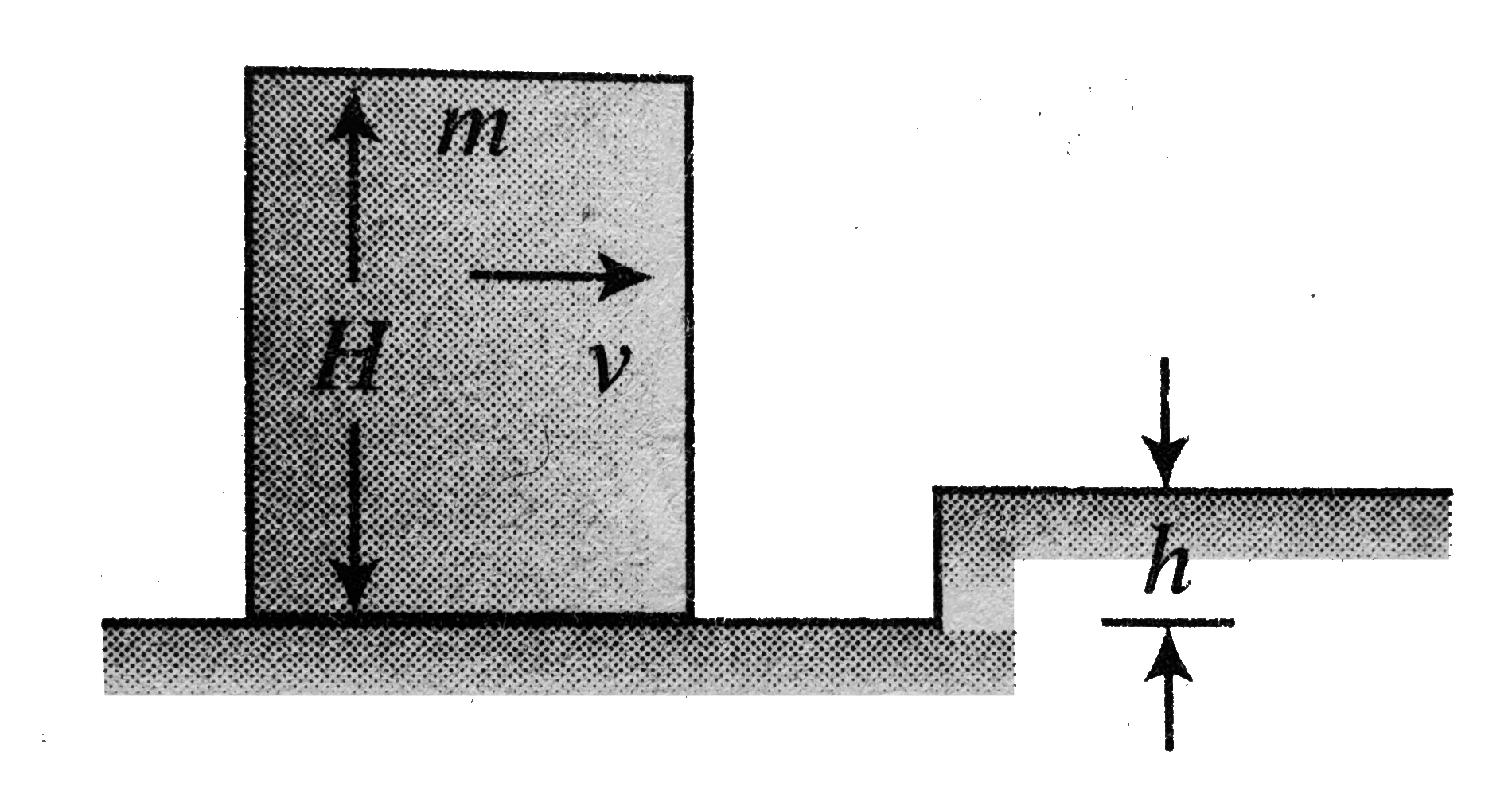 View Solution
View SolutionThe block on the loop shown slides without friction. At what height from A it starts so that it passes against the track at B with a net upward force equal to its own weight? The radius of the loop is R.
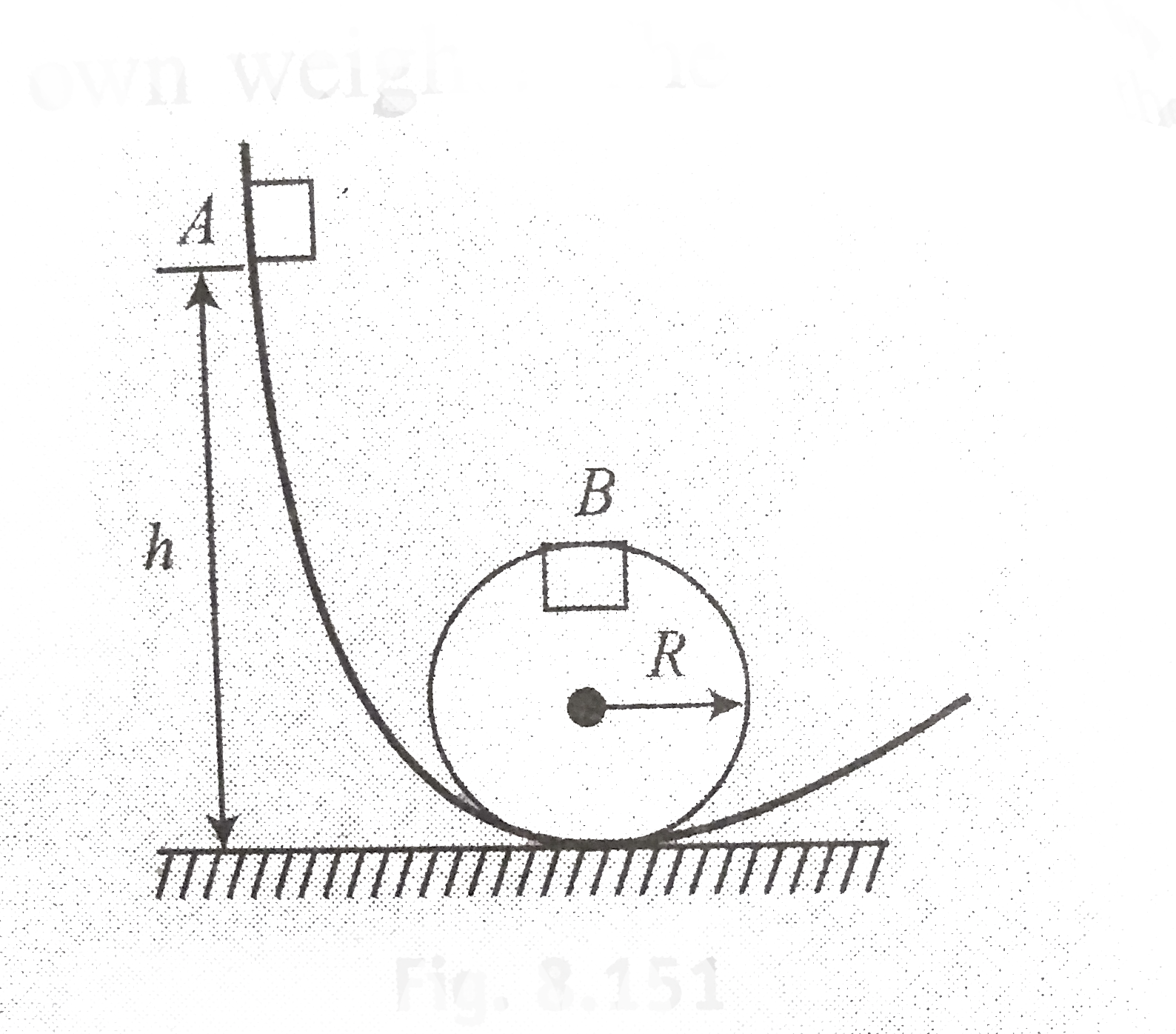 View Solution
View SolutionA man wants to slide down a block of mass m which is kept on a fixed inclined plane of inclination 30∘ as shown in the figure .Initially the block is not sliding .
To just start sliding the man pushed the block down the inclined with a force F. Now , the block starts accelerating. To move it downwards with conatant speed the man starts pulling the block with same force. Surface are such that ratio of maximum static friction to kinetic friction is 2 Now, answer the following questions.

What is the value of μs, the coefficient of static friction?View SolutionA man wants to slide down a block of mass m which is kept on a fixed inclined plane of inclination 30∘ as shown in the figure .Initially the block is not sliding .
To just start sliding the man pushed the block down the inclined with a force F. Now , the block starts accelerating. To move it downwards with conatant speed the man starts pulling the block with same force. Surface are such that ratio of maximum static friction to kinetic friction is 2 Now, answer the following questions.

If the man wants to move the block up the inclined , what minimum force is required to start the motion?View Solution

