A horizontal 50 N force acts on a 2 kg crate which is at rest on a smooth horizontal surface. At the instant the particle has gone 2 m, the rate at which the force is doing work is :
2.5 W
25 W
100 W
500 W
The correct Answer is:D
To solve the problem, we need to find the rate at which the force is doing work on the crate after it has moved 2 meters. This rate is defined as power.
1. Identify the Given Data:
- Force (F) = 50 N
- Mass (m) = 2 kg
- Displacement (s) = 2 m
2. Calculate the Acceleration:
- According to Newton's second law, acceleration (a) can be calculated using the formula:
a=Fm
- Substituting the values:
a=50N2kg=25m/s2
3. Determine the Final Velocity:
- We can use the kinematic equation to find the final velocity (v) after the crate has moved 2 meters. The equation is:
v2=u2+2as
- Since the crate starts from rest, the initial velocity (u) = 0. Thus:
v2=0+2⋅25m/s2⋅2m
v2=100
v=√100=10m/s
4. Calculate the Instantaneous Power:
- The instantaneous power (P) can be calculated using the formula:
P=F⋅v
- Substituting the values we have:
P=50N⋅10m/s=500W
Final Answer:
The rate at which the force is doing work is 500 Watts.
---
- Force (F) = 50 N
- Mass (m) = 2 kg
- Displacement (s) = 2 m
- According to Newton's second law, acceleration (a) can be calculated using the formula:
a=Fm
- Substituting the values:
a=50N2kg=25m/s2
- We can use the kinematic equation to find the final velocity (v) after the crate has moved 2 meters. The equation is:
v2=u2+2as
- Since the crate starts from rest, the initial velocity (u) = 0. Thus:
v2=0+2⋅25m/s2⋅2m
v2=100
v=√100=10m/s
- The instantaneous power (P) can be calculated using the formula:
P=F⋅v
- Substituting the values we have:
P=50N⋅10m/s=500W
The rate at which the force is doing work is 500 Watts.
Similar Questions
A force acts for 8 s on a body of mass 5 kg at rest,on a smooth horizontal surface.The force then stops acting and the body describes 80 m in next 5 s .The force acting on body is
View SolutionA force acts for 8 s on a body of mass 5kg at rest,on a smooth horizontal surface.The force then stops acting and the body describes 80m in next 5s .The force acting on body is ?
View Solution
Knowledge Check
A horizontal force of 129.4 N is applied on a 10 kg block which rests on a horizontal surface. If the coefficient of friction is 0.3, the acceleration should be
A9.8m/s2B10m/s2C12.6m/s2D19.6ms2A block is resting over a smooth horizontal plane. A constant horizontal force starts acting on it at t=0. Which of the following graph is correct:
A B
B C
C D
D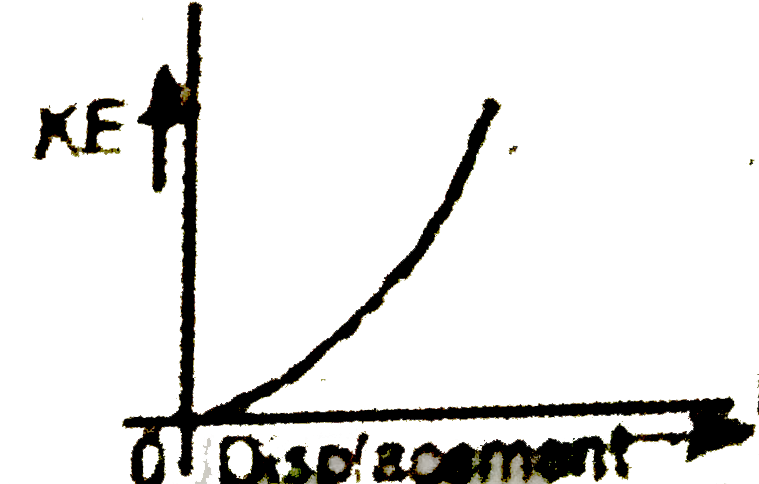
A force of 50N acts in the direction as shown in figure. The block of mass 5kg, resting on a smooth horizontal surface. Find out the acceleration of the block.
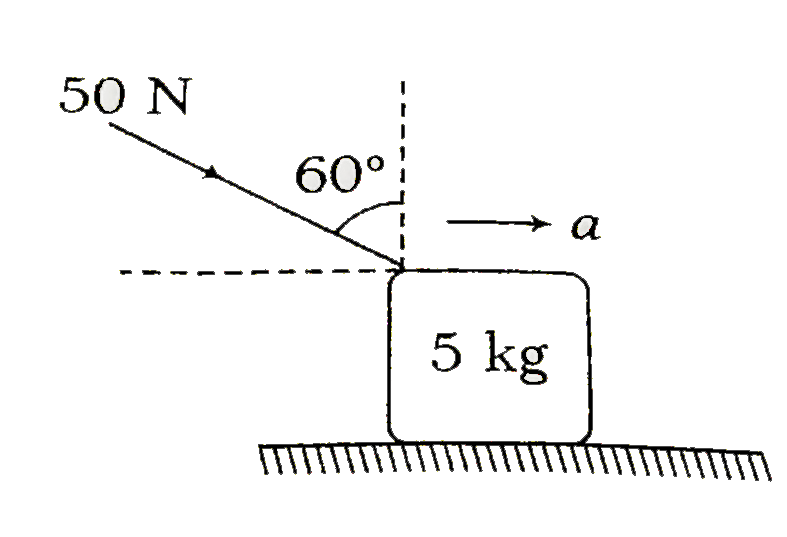 A5√3ms−2B2√3ms−2C15√3ms−2D3√3ms−2
A5√3ms−2B2√3ms−2C15√3ms−2D3√3ms−2
At the instant t=0, a force F=kt (k is a constant) acts on a small body of mass m resting on a smooth horizontal surface. The time, when the body leaves the surface is
View SolutionA horizontal force of 1.2kg is applied on a 1.5kg block, which rests on a horizontal surface If the coefficient of friction is 0.3 find the acceleration produced in the block.
View SolutionAdjoining figure shows a force of 40N acting at 30∘ to the horizontal on a body of mass 5kg resting on a smooth horizontal surface . Assuming that the acceleration of free-fall is 10ms−2, which of the following statements A,B,C,D,E is ( are ) correct ?
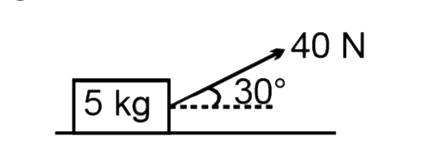
(1) The horizontal force acting on the body is 20 N
( 2) The weight of the 5 kg mass acts vertically downwards
(3) The net vertical force acting on the body is 30N
View SolutionA horizontal force ''F'' produces an acceleration of 6m/s−2 on a block resting on a smooth horizontal surface. The same force produces an acceleration of 3m/s−2 on a second block resting on a smooth horizontal surface. If the two blocks are tied together and the same force acts, the acceleration produced will be
View SolutionIn the given figure, the wedge is acted upon by a constant horizontal force F. The wedge is moving on a smooth horizontal surface. A ball of mass 'm' is at rest relative to the wedge. The ratio of forces exerted on 'm' by the wedge when F is acting, and when F is withdrawn, assuming no friction between the wedge and the ball, the ratio is equal to

View Solution
