Consider an oblique elastic collision between a moving ball and a stationary ball of the same mass. Both the balls move with the same speed after the collision. After the collision, the angle between the directions of motion of two balls is x degree. Find the value of x.
The correct Answer is:90
To solve the problem of finding the angle x between the directions of motion of two balls after an oblique elastic collision, we can follow these steps:
Step 1: Understand the scenario
We have two balls of equal mass. One ball is moving with an initial velocity v0 at an angle α to the horizontal, while the other ball is stationary. After the collision, both balls move with the same speed.
Step 2: Analyze the collision
Since the collision is elastic, both momentum and kinetic energy are conserved. We will analyze the velocities of the balls before and after the collision.
Step 3: Break down the initial velocity
The initial velocity v0 of the moving ball can be broken down into its components:
- Horizontal component: v0x=v0cosα
- Vertical component: v0y=v0sinα
Step 4: Apply conservation of momentum
For an elastic collision, the momentum along the line of impact is conserved. Let v1 and v2 be the velocities of the two balls after the collision. The equations for conservation of momentum can be written as:
1. v0x=v1+v2 (along the line of impact)
2. The vertical component remains unchanged for the first ball: v0y=v1y (for the first ball).
Step 5: Apply conservation of kinetic energy
The kinetic energy before and after the collision must also be equal:
12mv20=12mv21+12mv22
Step 6: Analyze the angles after collision
After the collision, the two balls move at an angle x to each other. Since they have the same speed after the collision, we can use trigonometric relationships to find the angle between their velocities.
Step 7: Solve for the angle x
From the conservation of momentum and the fact that the two balls move with the same speed after the collision, we can deduce that the angle x between their paths must be 90∘. This is because the momentum components must balance out in such a way that the two balls move perpendicularly to each other.
Conclusion
Thus, the value of x is:
x=90∘
---
We have two balls of equal mass. One ball is moving with an initial velocity v0 at an angle α to the horizontal, while the other ball is stationary. After the collision, both balls move with the same speed.
Since the collision is elastic, both momentum and kinetic energy are conserved. We will analyze the velocities of the balls before and after the collision.
The initial velocity v0 of the moving ball can be broken down into its components:
- Horizontal component: v0x=v0cosα
- Vertical component: v0y=v0sinα
For an elastic collision, the momentum along the line of impact is conserved. Let v1 and v2 be the velocities of the two balls after the collision. The equations for conservation of momentum can be written as:
1. v0x=v1+v2 (along the line of impact)
2. The vertical component remains unchanged for the first ball: v0y=v1y (for the first ball).
The kinetic energy before and after the collision must also be equal:
12mv20=12mv21+12mv22
After the collision, the two balls move at an angle x to each other. Since they have the same speed after the collision, we can use trigonometric relationships to find the angle between their velocities.
From the conservation of momentum and the fact that the two balls move with the same speed after the collision, we can deduce that the angle x between their paths must be 90∘. This is because the momentum components must balance out in such a way that the two balls move perpendicularly to each other.
Thus, the value of x is:
x=90∘
Similar Questions
Prove that in a two dimensional elastic collision of a moving ball with another stationary identical ball, the two balls move perpendicular to each other after collision?
View SolutionBall A of mass m strickes a stationary ball B of mass M and undergoes an elastic collision. After collision bill A has a speed one third of its initial speed. The ratio of M/m is
View Solution
Knowledge Check
- Question 1 - Select One or More
In an elastic collision between smooth balls :
AThe kinetic energy remain constantBThe linear momentum remains constantCThe final kinetic energy is equal to the initial kinetic energyDThe final linear momentum is equal to the initial linear momentum - Question 2 - Select One
A ball of mass m moving with a velocity v undergoes an oblique elastic collision with another ball of the same mass m but at rest. After the collision if the two balls move with the same speeds , the angle between their directions of motion will be:
A30∘B60∘C120∘D90∘ - Question 3 - Select One
Two balls of equal masses m each undergo oblique collision. If colision is perfectly elastic, then angle between their velocities after collision is
Aπ4Bπ3Cπ6Dπ2
Two identical billiard balls undergo an oblique elastic collision. Initially, one of the balls is stationary. If the initially stationary ball after collision moves in a direction which makes an angle of 37∘ with direction of initial motion of the moving ball, then the angle through which initially moving ball will be deflected is
View SolutionTwo balls each of mass 2kg (one at rest) undergo oblique collision is perfectly elastic, then the angle between their velocities after collision is
View SolutionA highly elastic ball moving at a speed of 3m/s approaches a wall moving towards it with a speed of 3m/s. After the collision. the speed of the ball will be
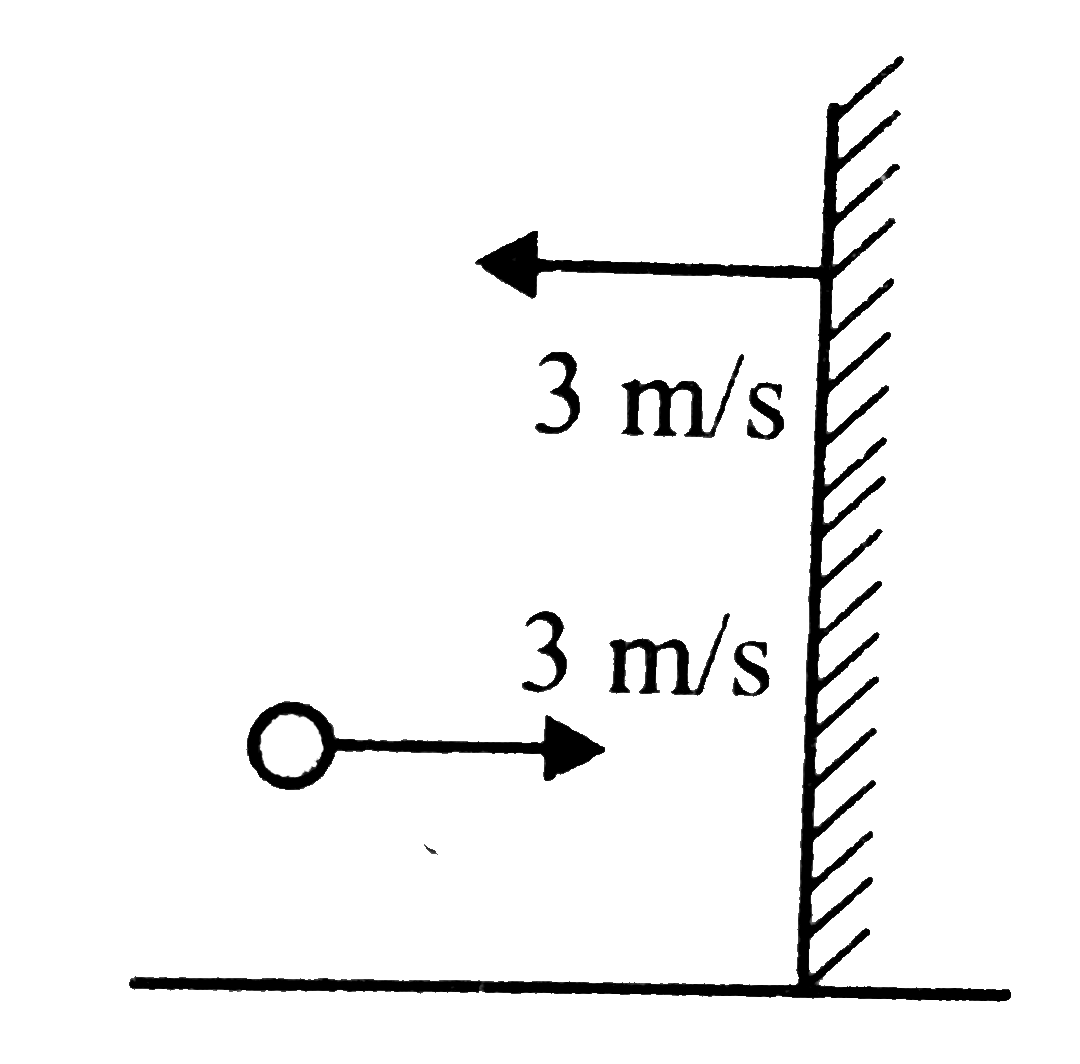 View Solution
View SolutionTwo billiard balls undergo a head-on collision. Ball 1 is twice as heavy as ball 2. Initially, ball 1 moves with a speed v towards ball 2 which is at rest. Immediately after the collision, ball 1 travels at a speed of v/3 in the same direction. What type of collision has occured ?
View SolutionTwo billiard balls undergo a head-on collision. Ball 1 is twice as heavy as ball 2. Initially, ball 1 moves with a speed v towards ball 2 which is at rest. Immediately after the collision, ball 1 travels at a speed of v/3 in the same direction. What type of collision has occured ?
View Solution

