A ball of mass 1 kg moving with velocity collides with a wall and after collision velocity of the ball is . Which of the following unit vectors is perpendicular to wall?
The correct Answer is:B
To find the unit vector that is perpendicular to the wall after a ball collides with it, we can follow these steps:
Step 1: Identify the initial and final velocities of the ball
The initial velocity of the ball before the collision is given as:
→vi=3^i+4^j
The final velocity of the ball after the collision is:
→vf=−2^i+6^j
Step 2: Determine the change in velocity
The change in velocity (Δ→v) can be calculated as:
Δ→v=→vf−→vi=(−2^i+6^j)−(3^i+4^j)=(−2−3)^i+(6−4)^j=−5^i+2^j
Step 3: Analyze the components of the velocity
The component of the velocity that is parallel to the wall will remain unchanged, while the component perpendicular to the wall will change direction.
Step 4: Define the unit normal vector to the wall
Let the unit vector perpendicular to the wall be:
^n=x^i+y^j
Since it is a unit vector, it must satisfy:
√x2+y2=1⇒x2+y2=1
Step 5: Set up the equations based on the reflection
The component of the initial velocity perpendicular to the wall will change direction, while the parallel component will remain the same. The reflection principle gives us:
Initial component along ^n=Final component along ^n
This can be expressed as:
→vi⋅^n=−→vf⋅^n
Step 6: Calculate the dot products
Calculating the dot products:
→vi⋅^n=(3^i+4^j)⋅(x^i+y^j)=3x+4y
−→vf⋅^n=−(−2^i+6^j)⋅(x^i+y^j)=(2^i−6^j)⋅(x^i+y^j)=2x−6y
Step 7: Set the equations equal
Setting the two expressions equal gives us:
3x+4y=2x−6y
Rearranging this gives:
x+10y=0⇒x=−10y
Step 8: Substitute into the unit vector equation
Substituting x=−10y into the unit vector equation:
(−10y)2+y2=1⇒100y2+y2=1⇒101y2=1⇒y2=1101⇒y=±1√101
Thus,
x=−10y=∓10√101
Step 9: Form the unit vector
The unit vector perpendicular to the wall is:
^n=(−10√101^i+1√101^j) or (10√101^i−1√101^j)
Step 10: Conclusion
Thus, the unit vector perpendicular to the wall can be expressed as:
^n=1√101(−10^i+1^j) or 1√101(10^i−1^j)
The initial velocity of the ball before the collision is given as:
→vi=3^i+4^j
The final velocity of the ball after the collision is:
→vf=−2^i+6^j
The change in velocity (Δ→v) can be calculated as:
Δ→v=→vf−→vi=(−2^i+6^j)−(3^i+4^j)=(−2−3)^i+(6−4)^j=−5^i+2^j
The component of the velocity that is parallel to the wall will remain unchanged, while the component perpendicular to the wall will change direction.
Let the unit vector perpendicular to the wall be:
^n=x^i+y^j
Since it is a unit vector, it must satisfy:
√x2+y2=1⇒x2+y2=1
The component of the initial velocity perpendicular to the wall will change direction, while the parallel component will remain the same. The reflection principle gives us:
Initial component along ^n=Final component along ^n
This can be expressed as:
→vi⋅^n=−→vf⋅^n
Calculating the dot products:
→vi⋅^n=(3^i+4^j)⋅(x^i+y^j)=3x+4y
−→vf⋅^n=−(−2^i+6^j)⋅(x^i+y^j)=(2^i−6^j)⋅(x^i+y^j)=2x−6y
Setting the two expressions equal gives us:
3x+4y=2x−6y
Rearranging this gives:
x+10y=0⇒x=−10y
Substituting x=−10y into the unit vector equation:
(−10y)2+y2=1⇒100y2+y2=1⇒101y2=1⇒y2=1101⇒y=±1√101
Thus,
x=−10y=∓10√101
The unit vector perpendicular to the wall is:
^n=(−10√101^i+1√101^j) or (10√101^i−1√101^j)
Thus, the unit vector perpendicular to the wall can be expressed as:
^n=1√101(−10^i+1^j) or 1√101(10^i−1^j)
Similar Questions
A ball of mass m, travelling with velocity 2ˆi+3ˆj receives an impulse −3mˆi. What is the velocity of the ball immediately afterwards?
View SolutionA particle of mass m moving with a velocity (3ˆi+2ˆj)ms−1 collides with another body of mass M and finally moves with velocity (−2ˆi+ˆj)ms−1. Then during the collision
View Solution
Knowledge Check
- Question 1 - Select One
A ball A moving with momentum 2ˆi+4ˆj collides with identical ball B moving with momentum 6ˆj . After collision momentum of ball B is 10ˆj . Which of the following statement is correct?
AAfter collision momentum of A is 4ˆiBAfter collision momentum of A is parallel to momentum of BCAfter collision momentum of A is 2ˆiDIf →PAand→PB are momenta of balls A and B, then Δ(∣∣→PA∣∣+∣∣→PB∣∣)=0 - Question 2 - Select One
A small sphere of mass m=2kg moving with a velocity ¯u=4ˆi−7ˆjm/s colides with a smooth wall and returns with a velocity ¯v=−ˆi+3ˆjm/s. The magnitude of the impulse received by the ball is .
A5kgms−1B10√5kgms−1C20kgms−1D15kgms−1 - Question 3 - Select One
A ball of mass m moving with velocity →u=uxˆi+uyˆj hits a vertical wall of infinite mass as shown in the figure. The ball slips up along the wall for the duration of collision and there is friction between the ball and the wall. Neglect the effect of gravity. Pick up the correct alternative.
 AThe wall provides the ball with net impulse along the negative x-axis for the duration of collision.BThe collision change only the x-component of velocity of thr ballCThe collision change only the y-component of velocity of thr ballDThe impulse provides by friction force to the ball for the duration of collision cannot be neglected in comparison to impulse provided by normal reaction
AThe wall provides the ball with net impulse along the negative x-axis for the duration of collision.BThe collision change only the x-component of velocity of thr ballCThe collision change only the y-component of velocity of thr ballDThe impulse provides by friction force to the ball for the duration of collision cannot be neglected in comparison to impulse provided by normal reaction
A vector is given by →V=(8.0ˆi+2.0ˆj)m/s . What will be the unit vector perpendicular to →V?
View SolutionA small sphere of mass m=1kg is moving with a velocity (4ˆi−ˆj)m/s. it hits a fixed smooth wall and rebounds with velocity (ˆi+3ˆj)m/s. The coefficient of restitution between the sphere and the wall is n/16. Find the value of n.
View SolutionA ball of mass m moving with velocity v0 collides with a wall as shown in Fig. After impact it rebounds with a velocity' (v0)/2The component of impulse acting on the ball along the wall is
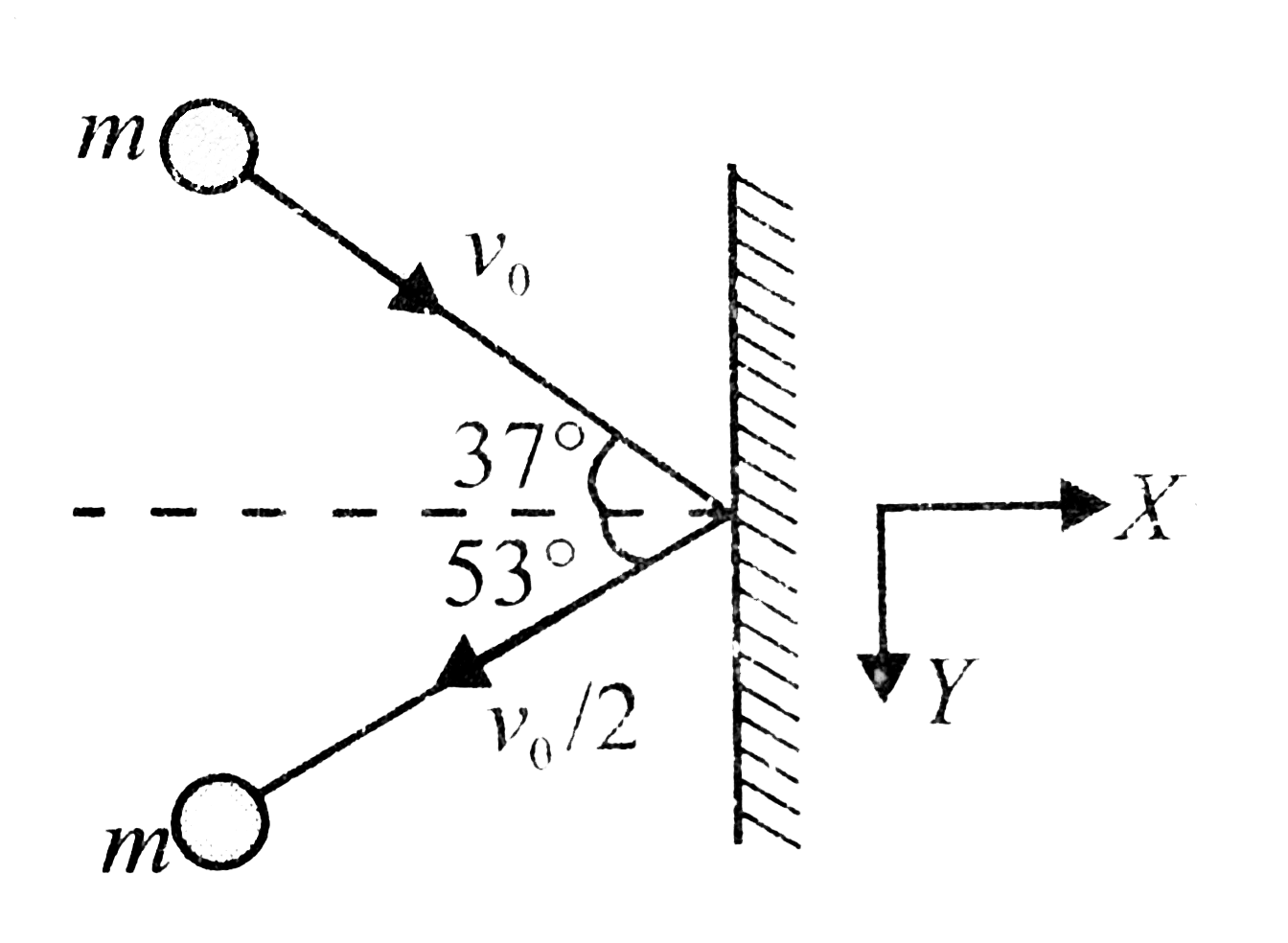 View Solution
View SolutionA small sphere of mass 1kg is moving with a velocity (6ˆi+ˆj)m/s . It hits a fixed smooth wall and rebounds with velocity (4ˆi+ˆj)m/s. The coefficient of restitution between the sphere and the wall is
View SolutionA body of mass 2 kg is moving with a velocity of →u=3ˆi+4ˆjm/s. A steady force →F=ˆi−2ˆj N begins to act on it. After four seconds, the body will be moving along.
View Solution

