Question

A thin rod of length L is lying along the x-axis with its ends at x = 0 and x = L. Its linear density (mass/length) varies with x as $k{\left(\frac{x}{L}\right)}^n$ where n can be zero or any positive number. If the position $X_{CM}$ of the centre of mass of the rod is plotted against n, which of the following graphs best approximates the dependence of $X_{CM}$ on n?

Options

A.
B.
C.
D.

Answer

A

Explanation

To find the position of the center of mass $$X_{CM}$$ of the thin rod with a varying linear density, we will follow these steps:

Step 1: Define the linear density
The linear density of the rod is given by:
\( \lambda(x) = k \left( \frac{x}{L} \right)^n \)
where \( k \) is a constant, \( L \) is the length of the rod, and \( n \) can be 0 or any positive number.

Step 2: Express the mass element
The mass element \( dm \) of a small segment of the rod of length \( dx \) at position \( x \) is given by:
\( dm = \lambda(x) \, dx = k \left( \frac{x}{L} \right)^n \, dx \)

Step 3: Calculate the total mass of the rod
The total mass \( M \) of the rod can be calculated by integrating \( dm \) from 0 to \( L \):
\( M = \int_0^L dm = \int_0^L k \left( \frac{x}{L} \right)^n \, dx \)
This simplifies to:
\( M = k \int_0^L \left( \frac{x^n}{L^n} \right) \, dx = \frac{k}{L^n} \int_0^L x^n \, dx \)
The integral \( \int_0^L x^n \, dx \) evaluates to:
\( \int_0^L x^n \, dx = \frac{L^{n+1}}{n+1} \)
Thus, the total mass becomes:
\( M = \frac{k}{L^n} \cdot \frac{L^{n+1}}{n+1} = \frac{kL}{n+1} \)

Step 4: Calculate the center of mass \( X_{CM} \)
The center of mass \( X_{CM} \) is given by:
\( X_{CM} = \frac{1}{M} \int_0^L x \, dm = \frac{1}{M} \int_0^L x \cdot k \left( \frac{x}{L} \right)^n \, dx \)
This can be simplified to:
\( X_{CM} = \frac{1}{M} \cdot k \int_0^L \frac{x^{n+1}}{L^n} \, dx = \frac{1}{M} \cdot \frac{k}{L^n} \cdot \frac{L^{n+2}}{n+2} \)
Substituting \( M \) from the previous step:
\( X_{CM} = \frac{1}{\frac{kL}{n+1}} \cdot \frac{kL^{n+2}}{(n+2)L^n} = \frac{L^{n+2}}{L(n+1)(n+2)} = \frac{L(n+1)}{(n+2)} \)

Step 5: Analyze the behavior of \( X_{CM} \) with respect to \( n \)
The expression for the center of mass is:
\( X_{CM} = \frac{L(n+1)}{(n+2)} \)
As \( n \) increases, the ratio \( \frac{n+1}{n+2} \) approaches 1, meaning \( X_{CM} \) approaches \( L \).

Step 6: Graphical representation
- For \( n = 0 \): \( X_{CM} = \frac{L(1)}{(2)} = \frac{L}{2} \)
- As \( n \) increases, \( X_{CM} \) approaches \( L \).

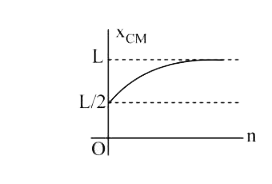
Thus, the graph of \( X_{CM} \) against \( n \) will start at \( \frac{L}{2} \) when \( n = 0 \) and will asymptotically approach \( L \) as \( n \) increases.

Final Answer
The graph that best represents the dependence of \( X_{CM} \) on \( n \) will start at \( \frac{L}{2} \) and approach \( L \) as \( n \) increases.