Four particles A, B, C and D with masses $m_{A} = m, m_{B} = 2 m, m_{C} = 3 m and m_{D} = 4 m$ are at the corners of a square. They have accelerations of equal magnitude with directions as shown. The acceleration of the centre of mass of the particles is:

A

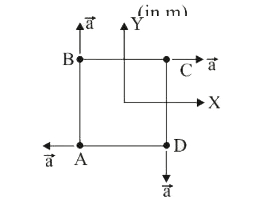
$\frac{a}{5} (ˆ i - ˆ j)$

B

$a (ˆ i + ˆ j)$

C

$\frac{a}{5} (ˆ i + ˆ j)$

D

zero

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

${¯ a}_{C M} = \frac{m_{1} {¯ a}_{1} + m_{3} {¯ a}_{2} + m_{3} {¯ a}_{3} + m_{4} {¯ a}_{4}}{m_{1} + m_{2} + m_{3} + m_{4}} = \frac{m (- a ˆ i) + 2 m (a ˆ j) + 3 m (a ˆ i) + 4 m (- a ˆ j)}{m + 2 m + 3 m + 4 m} = \frac{2 a ˆ i - 2 a ˆ j}{10} = \frac{a}{5} (ˆ i - ˆ j)$

|

Updated on:21/07/2023

Class 12 PHYSICS ENERGY & MOMENTUM

Similar Questions

Knowledge Check

Question 1 - Select One
Four particle of masses $m_{1} = 2 m, m_{2} = 4 m, m_{3} = m and m_{4}$ are placed at four corners of a square. What should be the value of $m_{4}$ so that the centres of mass of all the four particle are exactly at the centre of the square ?

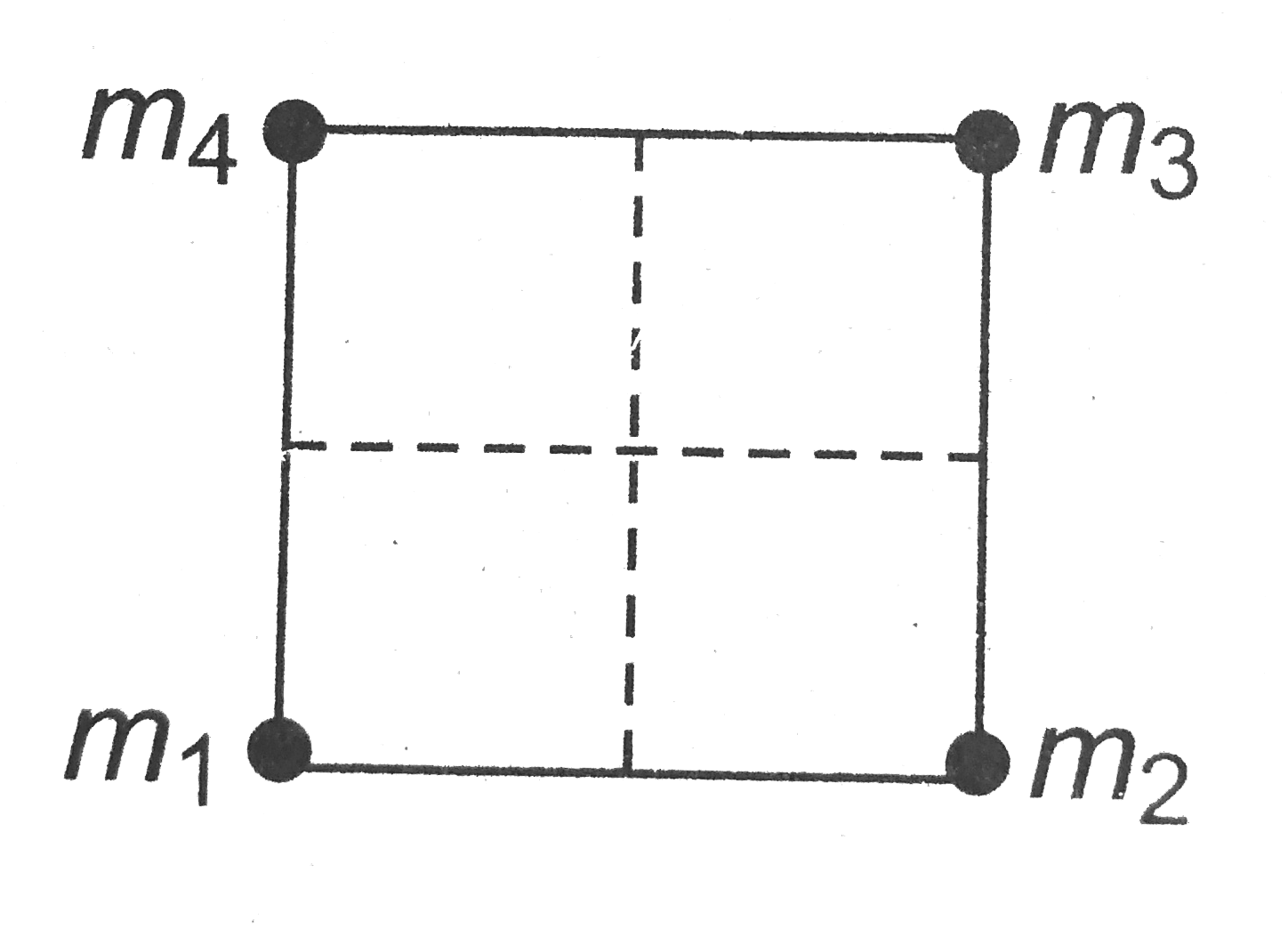A3 m
B5 m
C8 m
Dnone of these
Question 2 - Select One
In the figure shown, the acceleration of block of mass $m_{2}$ is $2 m / s^{2}$ . The acceleration of $m_{1}$ $:$

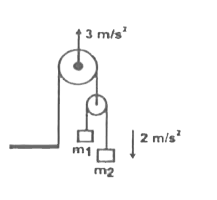Awill be $8 m / s^{2}$ upward
Bwill be $4 m / s^{2}$ upward
Cwill be $14 m / s^{2}$ upward
DThe value depends upon actual values of $m_{1}$ and $m_{2}$
Question 3 - Select One
Four particles of masses m, 2m, 3m and 4m are arranged at the corners of a parallelogram with each side equal to a and one of the angle between two adjacent sides as $60^{\circ}$ The parallelogram lies in the x-y plane with mass m at the origin and 4m on the r-axis. The centre of mass of the arrangement will be located at
A $(\frac{\sqrt{3}}{2} a, 0.95 a)$
B $(0.95 a, \frac{\sqrt{3}}{4} a)$
C $(\frac{3 a}{4}, \frac{a}{2})$
D $(\frac{a}{2}, \frac{3 a}{4})$

Recommended Questions

Home
Ask Doubt
Profile