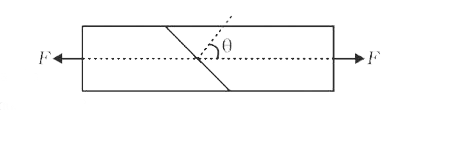
A bar of cross-section A is subjected to equal and opposite tensile forces at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar .
(i) What is the tensile stress on this plane?
(ii) What is the shearing stress on this plane?
(iii) For what value of θ is the tensile stress maximum
(iv) For what value of θ is the shearing stress maximum?
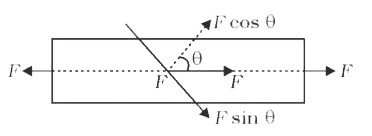
(i) The resolved part of F along the normal is the tensile force on this plane and the resolved part parallel to the plane is the shearing force on the plane.
∴ Area of plane section =Asecθ
Tensile stress =ForceArea=FcosθAsecθ =FAcos2θ
(ii) Shearing stress applied on the plane
So , F=Fsinθ
Shearing stress =ForceArea=FsinθAsecθ=FAsinθcosθ
=F2Asin2θ [∵sin2θ=2sinθcosθ]
(iii) Tensile stress will be maximum when cos2θ is maximum i.e., cosθ=1orθ=0∘ (iv) Shearing stress will be maximum when sin2θ is maximum i.e . sin2θ=1 or 2θ=90∘orθ=45∘ .
Similar Questions
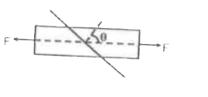
A bar of cross section A is subjected to equal and opposite tensile force at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar.

a. What is the tensile stress on the plane?
b. What is the shearing stress on the this plane?
c. For what value of θ is the tensile stress maximum?
d. For what value of θ is the shearing stress maximum?
View SolutionA bar of cross-section A is subjected two equal and opposite tensile forces at its ends consider a plane section of the bar whose makes an angle θ with the axis of the bar.
(a) what is the tensile stress on this plane ?
(b)what is the shearing stress on this plane ?
(c )for what value of θ is the tensile stress is maximum ?
(d) for what value of θ is the shearing stress maximum ?
View Solution
Knowledge Check
A bar of cross- sectional area A is is subjected two equal and opposite tensile forces at its ends as shown in figure. Consider a plane BB' making an angle θ with length
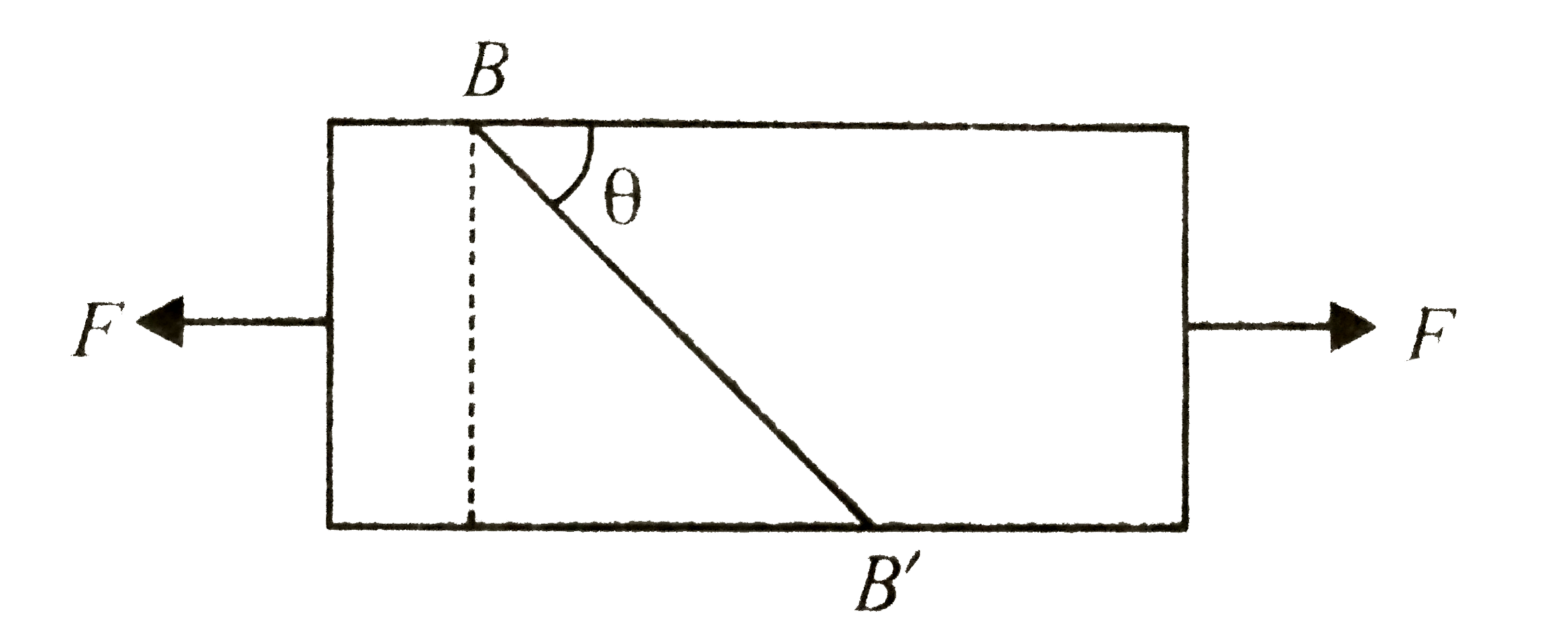 AtanθBsecθCcotθDcosθ
AtanθBsecθCcotθDcosθIn the above problem, for what angle is the shearing stress a maximum?
A30∘B45∘C60∘D90∘In the question rumber 66, for what value of θ, shearing stress is maximum?
A0∘B30∘C45∘D90∘
A bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in figure.
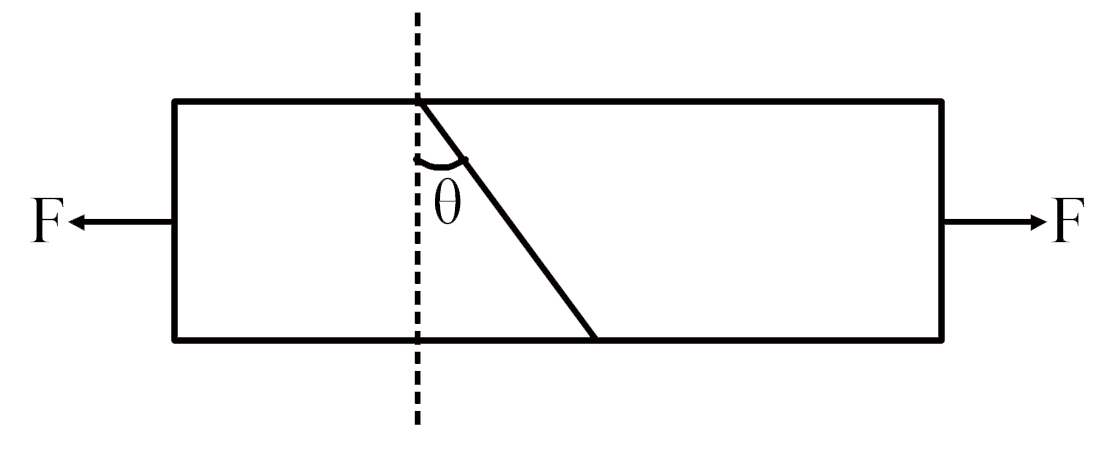
The tensile stress at this plane in terms of F, A and θ is
View SolutionA bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in figure.
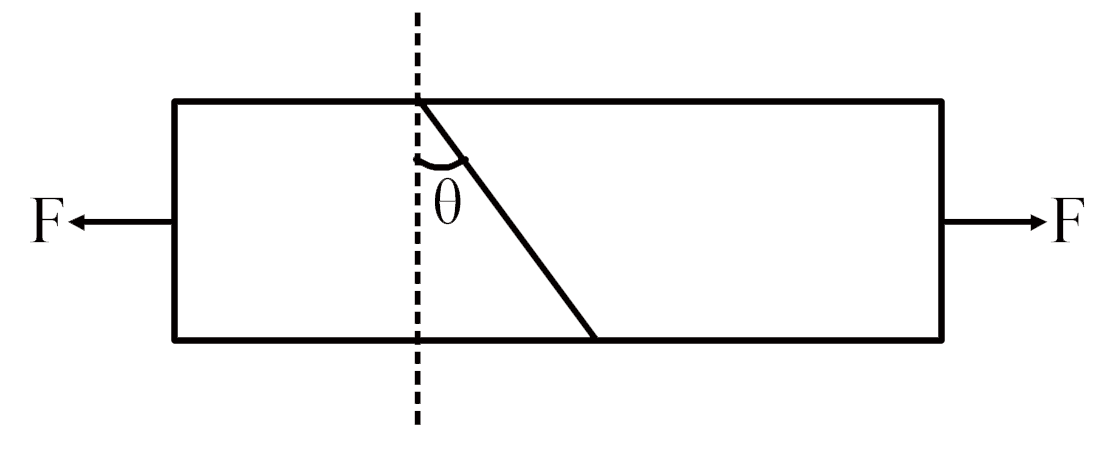
The shearing stress at the plane, in terms of F, A and θ is
View SolutionA bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in figure.
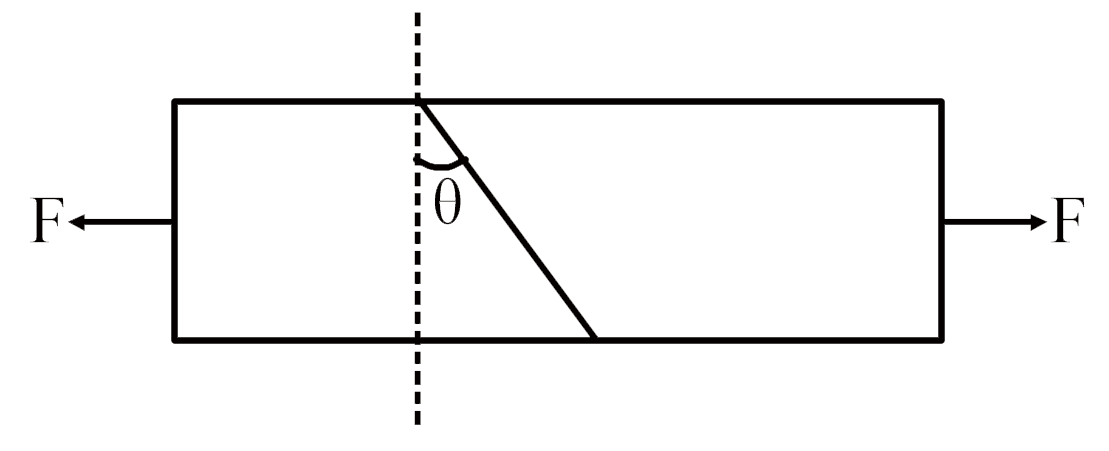
In the above problem, for what value of θ is the tensile stress maximum ?
View SolutionA steel bar of cross section A is subjected to two equal and opposite pulling forces at the two ends. If there is a plane through the bar making an angle α as shown, find
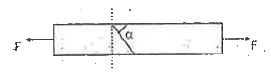
the shearing stress at this plane
View SolutionConsider a long steel bar under a tensile stress due to forces F, acting at the edges along the length of the bar

Consider a plane making an angle θ with the length. What are the tensile and shering stresses on this plane ? (a) For what angle is the tensile stress a maximum ? (b) For what angle is the shearing stress a maximum ?
View Solution