Inner and outer surfaces of a cylinder are maintained at temperature 4T and T respectively. Heat flows radially from inner surface of radius R to outer surface of radius 4R. Radial distance from the center where temperature is 2T.
2 R
25/3R
24/3R
3 R
The correct Answer is:C
To solve the problem of finding the radial distance from the center of a cylinder where the temperature is 2T, we can follow these steps:
Step 1: Understand the Setup
We have a cylinder with:
- Inner surface temperature = 4T
- Outer surface temperature = T
- Inner radius = R
- Outer radius = 4R
Step 2: Set Up the Heat Flow Equation
The heat flow through the cylinder can be described by Fourier's law of heat conduction:
H=−kAdθdr
where:
- H = heat flow rate
- k = thermal conductivity
- A = area through which heat is flowing
- dθ = temperature difference
- dr = radial distance
Step 3: Determine the Area
For a cylindrical shell at radius r, the area A is given by:
A=2πrL
where L is the length of the cylinder (assumed constant).
Step 4: Write the Heat Flow Equation
Substituting the area into the heat flow equation, we have:
H=−k(2πrL)dθdr
Step 5: Rearranging the Equation
Rearranging gives:
H=−2πkLrdθdr
This can be rearranged to:
dθdr=−Hr2πkL
Step 6: Integrate Both Sides
Integrate both sides from R to r for the temperature and from R to 4R for the radius:
∫θ4Tdθ=−H2πkL∫rR1rdr
Step 7: Evaluate the Integrals
The left side integrates to:
θ−4T
The right side integrates to:
−H2πkLln(rR)
Thus, we have:
θ−4T=−H2πkLln(rR)
Step 8: Set Up the Equation for Temperature 2T
Now, we want to find r when θ=2T:
2T−4T=−H2πkLln(rR)
This simplifies to:
−2T=−H2πkLln(rR)
Step 9: Solve for r
Rearranging gives:
ln(rR)=4πkLTH
Exponentiating both sides:
rR=e4πkLTH
Thus:
r=Re4πkLTH
Step 10: Find the Value of r
Using the established relationship, we can find the exact value of r in terms of R.
Final Answer
The radial distance r where the temperature is 2T is:
r=243R
We have a cylinder with:
- Inner surface temperature = 4T
- Outer surface temperature = T
- Inner radius = R
- Outer radius = 4R
The heat flow through the cylinder can be described by Fourier's law of heat conduction:
H=−kAdθdr
where:
- H = heat flow rate
- k = thermal conductivity
- A = area through which heat is flowing
- dθ = temperature difference
- dr = radial distance
For a cylindrical shell at radius r, the area A is given by:
A=2πrL
where L is the length of the cylinder (assumed constant).
Substituting the area into the heat flow equation, we have:
H=−k(2πrL)dθdr
Rearranging gives:
H=−2πkLrdθdr
This can be rearranged to:
dθdr=−Hr2πkL
Integrate both sides from R to r for the temperature and from R to 4R for the radius:
∫θ4Tdθ=−H2πkL∫rR1rdr
The left side integrates to:
θ−4T
The right side integrates to:
−H2πkLln(rR)
Thus, we have:
θ−4T=−H2πkLln(rR)
Now, we want to find r when θ=2T:
2T−4T=−H2πkLln(rR)
This simplifies to:
−2T=−H2πkLln(rR)
Rearranging gives:
ln(rR)=4πkLTH
Exponentiating both sides:
rR=e4πkLTH
Thus:
r=Re4πkLTH
Using the established relationship, we can find the exact value of r in terms of R.
The radial distance r where the temperature is 2T is:
r=243R
Similar Questions
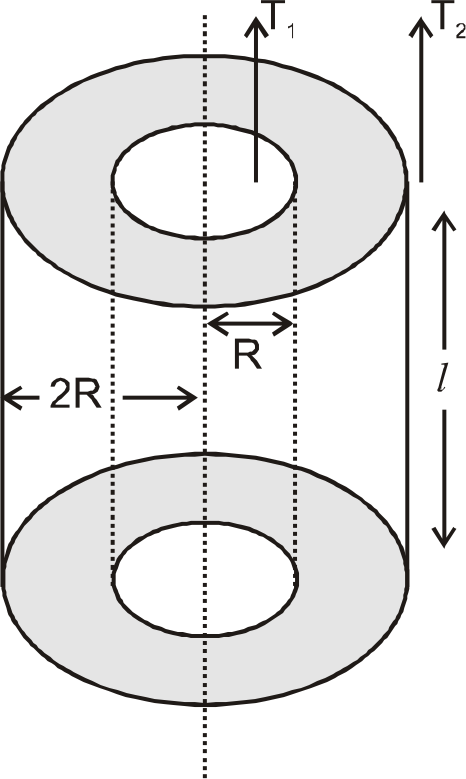
Inner surfaec of a cylindrical shell of length l and of material of thermal conductivity k is kept at constant temperature T1 and outer surface of the cylinder is kept at constant temperature T2 such that (T1>T2) as shown in figure. heat flows from inner surface to outer surface radially outward. inner and outer radii of the shell are R and 2R resspectively. Due to lack of space this cylinder has to be replaced by a smaller cylinder of length l2 inner and outer radii R4 and R respectively and thermal conductivity of material nk. if rate of radially outward heat flow remains same for same temperatures of inner and outer surface i.e., T1 and T2 then find the value of n.View SolutionA metallic cylindrical shell of length 50 cm has inner radius of 3 cm and outer radius of 6 cm. If the inner and outer surfaces of the cylinder are maintained at 0∘C and 80∘C , respectively, then find the rate of flow of heat from the outer surface to the inner surface. Take, thermal conductivity of metal =69.3Wm−1k−1
View Solution
Knowledge Check
- Question 1 - Select One
A number of droplets, each of radius r, combine to form a drop of radius R. If T is the surface tension, the rise in temperature will be
A2TrB3TRC2T[1r−1R]D3T[1r−1R] - Question 2 - Select One
If charge q induced on outer surface of sphere of radius R, then intensity at point P at distance S from centre is
Ainversely proportional to (S+R)2Binversely proportional to R2.Cinversely proportional to S2.Ddirectly proportional to S2. - Question 3 - Select One
Inner and outer radii of a spool are r and R respectively. A thread is wound over its inner surface and placed over a rough horizontal surface. Then:
 .AThread unwinds, spool rotates anticlockwise and friction acts leftwardsBThread winds, spool rotates clockwise and friction acts leftwardsCThread winds, spool moves to the right and friction act rightwardsDThread winds, spool moves to the right and friction does not come into existence
.AThread unwinds, spool rotates anticlockwise and friction acts leftwardsBThread winds, spool rotates clockwise and friction acts leftwardsCThread winds, spool moves to the right and friction act rightwardsDThread winds, spool moves to the right and friction does not come into existence
Heat flows radially outwards through a spherical shell of outside radius R2 and inner radius R1. The temperature of inner surface of shell is θ1 and that of outer is θ2. At what radial distance from centre of shell the temperature is just half way between θ1andθ2?
View SolutionAssuming the sun to have a spherical outer surface of radius r, radiating like a black body at temperature t∘c, the power received by a unit surface, (normal to the incident rays) at a distance R from the centre of the sun is
where σ is the Stefan's constant.View SolutionAssuming the sun to have a spherical outer surface of radius r, radiating like a black body at temperature t∘c, the power received by a unit surface, (normal to the incident rays) at a distance R from the centre of the sun is
where σ is the Stefan's constant.View SolutionAssuming the sun to have a spherical outer surface of radius r radiating like a black body at temperature t∘C. The power received by a unit surface (normal to the incident rays) at a distance R from the centre of the sun is
where σ is the Stefan's constant.View SolutionIf charge q is induced on outer surface of sphere of radius R, then intensity at a point P at a distance S from its centre is
View Solution

