Question

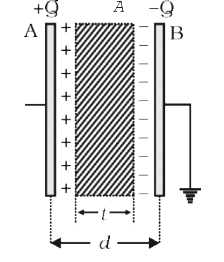
Find an expression for the capacitance of a parallel plate capacitor when a dielectric slab of dielectric constant K and thickness $t=\frac{d}{2}$ but the same area on the plates is inserted between the the capacitors plate. (d=separation between the plates)

Explanation

To find the expression for the capacitance of a parallel plate capacitor with a dielectric slab inserted, we can follow these steps:

Step 1: Understand the Configuration
We have a parallel plate capacitor with:
- Plate area \( A \)
- Plate separation \( d \)
- A dielectric slab of thickness \( t = \frac{d}{2} \) and dielectric constant \( K \) inserted between the plates.

Step 2: Determine the Effective Configuration
The capacitor can be thought of as two capacitors in series:
1. The first capacitor (Capacitor 1) has a dielectric slab of thickness \( t = \frac{d}{2} \) and dielectric constant \( K \).
2. The second capacitor (Capacitor 2) has a vacuum (or air) thickness of \( d - t = \frac{d}{2} \).

Step 3: Calculate the Capacitance of Each Section
- Capacitance of Capacitor 1 (with dielectric):
\( C_1 = \frac{K \epsilon_0 A}{t} = \frac{K \epsilon_0 A}{\frac{d}{2}} = \frac{2K \epsilon_0 A}{d} \)

- Capacitance of Capacitor 2 (vacuum):
\( C_2 = \frac{\epsilon_0 A}{\frac{d}{2}} = \frac{2 \epsilon_0 A}{d} \)

Step 4: Combine the Capacitances in Series
For capacitors in series, the total capacitance \( C \) is given by:
\( \frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} \)

Substituting the values of \( C_1 \) and \( C_2 \):
\( \frac{1}{C} = \frac{1}{\frac{2K \epsilon_0 A}{d}} + \frac{1}{\frac{2 \epsilon_0 A}{d}} \)

Step 5: Simplify the Expression
Calculating the right-hand side:
\( \frac{1}{C} = \frac{d}{2K \epsilon_0 A} + \frac{d}{2 \epsilon_0 A} \)
Finding a common denominator:
\( \frac{1}{C} = \frac{d}{2 \epsilon_0 A} \left( \frac{1}{K} + 1 \right) \)
Thus,
\( \frac{1}{C} = \frac{d}{2 \epsilon_0 A} \left( \frac{1 + K}{K} \right) \)

Step 6: Final Expression for Capacitance
Taking the reciprocal to find \( C \):
\( C = \frac{2 \epsilon_0 A K}{d(1 + K)} \)

Conclusion
The expression for the capacitance of the parallel plate capacitor with the dielectric slab inserted is:
\( C = \frac{2 \epsilon_0 A K}{d(1 + K)} \)