An electron in the ground state of hydrogen atom is revolving in anti-clock wise direction in a circular orbit. The atom is placed in a magnetic filed such that the normal to the electron orbit makes an angle of 30° with the magnetic field. Find the torque experienced by the orbiting electron.
To find the torque experienced by the orbiting electron in a hydrogen atom placed in a magnetic field, we can follow these steps:
Step 1: Understand the System
The electron is revolving in a circular orbit in an anti-clockwise direction. The angle between the normal to the orbit and the magnetic field is given as 30∘.
Step 2: Identify the Torque Formula
The torque (τ) experienced by a magnetic moment (M) in a magnetic field (B) is given by the formula:
τ=M×B×sin(θ)
where θ is the angle between the magnetic moment and the magnetic field.
Step 3: Calculate the Magnetic Moment
The magnetic moment (M) for an electron revolving in a circular orbit can be calculated using:
M=I⋅A
where I is the current and A is the area of the orbit.
Step 4: Determine the Current
The current (I) due to the revolving electron can be expressed as:
I=qT
where q is the charge of the electron and T is the time period of revolution.
Step 5: Calculate the Time Period
The time period T for an electron in a circular orbit can be calculated using:
T=2πrv
where r is the radius of the orbit and v is the velocity of the electron.
Step 6: Calculate the Area
The area A of the circular orbit is given by:
A=πr2
Step 7: Substitute Values
Substituting I and A into the magnetic moment formula:
M=I⋅A=(qT)⋅πr2
Step 8: Substitute for Torque
Now substituting M into the torque formula:
τ=M⋅B⋅sin(30∘)
Since sin(30∘)=12, we can simplify:
τ=12M⋅B
Step 9: Final Expression
Using the expression for the magnetic moment of an electron in a hydrogen atom:
M=eh4πme
where e is the charge of the electron, h is Planck's constant, and me is the mass of the electron, we can write:
τ=12⋅eh4πme⋅B
Step 10: Conclusion
Thus, the torque experienced by the orbiting electron is:
τ=ehB8πme
---
The electron is revolving in a circular orbit in an anti-clockwise direction. The angle between the normal to the orbit and the magnetic field is given as 30∘.
The torque (τ) experienced by a magnetic moment (M) in a magnetic field (B) is given by the formula:
τ=M×B×sin(θ)
where θ is the angle between the magnetic moment and the magnetic field.
The magnetic moment (M) for an electron revolving in a circular orbit can be calculated using:
M=I⋅A
where I is the current and A is the area of the orbit.
The current (I) due to the revolving electron can be expressed as:
I=qT
where q is the charge of the electron and T is the time period of revolution.
The time period T for an electron in a circular orbit can be calculated using:
T=2πrv
where r is the radius of the orbit and v is the velocity of the electron.
The area A of the circular orbit is given by:
A=πr2
Substituting I and A into the magnetic moment formula:
M=I⋅A=(qT)⋅πr2
Now substituting M into the torque formula:
τ=M⋅B⋅sin(30∘)
Since sin(30∘)=12, we can simplify:
τ=12M⋅B
Using the expression for the magnetic moment of an electron in a hydrogen atom:
M=eh4πme
where e is the charge of the electron, h is Planck's constant, and me is the mass of the electron, we can write:
τ=12⋅eh4πme⋅B
Thus, the torque experienced by the orbiting electron is:
τ=ehB8πme
Similar Questions
An electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in the circular orbit of radius R as shown in figure.
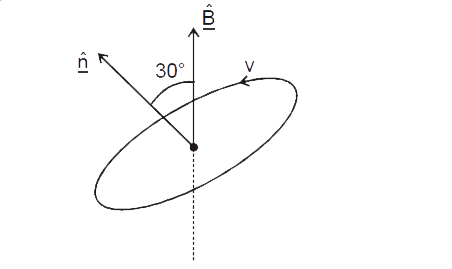
The atom is placed in a uniform magnetic induction B such that the plane normal of the electron orbit makes an angle 30∘ with the magnetic induction. Find the torque experienced by the orbiting electron.View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in the circular orbit of radius R as shown in figure.

The atom is placed in a uniform magnetic induction B such that the plane normal of the electron orbit makes an angle 30∘ with the magnetic induction. Find the torque experienced by the orbiting electron.View Solution
Knowledge Check
- Question 1 - Select One
An electron in the ground state of hydrogen atom is revolving in anticlockwise direction in the circular orbit of radius R. The atom is placed in a uniform magnetic induction B such that the plane normal of electron orbit makes an angle 30∘ with B, as shown in figure. The torque experienced by electron will be
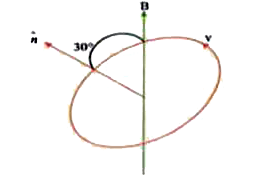 . AehB8πmBeh8πBmCeB8πmhDhB8πem
. AehB8πmBeh8πBmCeB8πmhDhB8πem - Question 2 - Select One
An electron in the ground state of hydrogen atom is revolving in anticlockwise direction in circular orbit of radius R. The orbital magnetic dipole moment of the electron will be
Aeh4πmBeh2πmCeh24πmDe2h4πm - Question 3 - Select One
An electron revolves in a circular orbit of radius r with angular speed ω . The magnetic field at the centre of electron orbit is
Aμ0eωπrBμ0eω4πrCμ0e2ω4πrDμ0eω2πr
An electron in the ground state of hydrogen atom is revolving in anticlock-wise direction in a circular orbit of radius R.
(i) Obtain an experssion for the orbital magnetic dipole moment of the electron.
(ii) The atom is placed in a uniform magnetic induction →B such that the plane - normal of the electron - orbit makes an angle of 30∘ with the magnetic induction . Find the torque experienced by the orbiting electron.
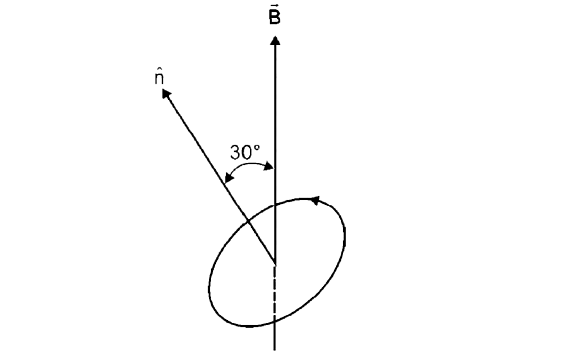 View Solution
View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in a circular orbit of radius R.

(i) The expression for the orbital magnetic moment of the electrton is ehnπm. Find n □
(ii) The atom is placed in a uniform magnetic induction B such that the normal to the plane of electron’s orbit makes an angle of 30∘ with the magnetic induction. The torque experienced by the orbiting electron is ehBnπm. Find n □View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in the circular orbit of radius R as shown in figure.
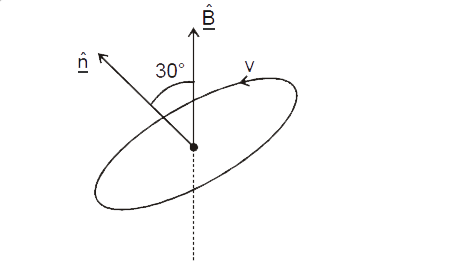
Obtain an expression for the orbital magnetic dipole moment of the electron.View SolutionWhen an electron in hydrogen atom revolves in stationary orbit, it
View SolutionIn the ground state, the electron in the hydrogen atom moves in a circular orbit of radius r0 . When the hydrogen atom goes in the second excited state, the radius of the electron orbit is increased by
View Solution

