A circular wire loop of radius R is placed in the X-Y plane with its centre at the origin. The loop carries a current I in the clockwise direction when viewed from a point on the positive Z-axis. A uniform magnetic field exists in the region . The magnitued of the magnetic force on the loop due to the magnetic field is . The value of n is______________.
The correct Answer is:2
To solve the problem, we need to calculate the magnetic force acting on a circular wire loop placed in a magnetic field. The loop carries a current in a specific direction, and we will use the relevant formulas to find the required value of n.
1. Understanding the Setup:
- We have a circular wire loop of radius R centered at the origin in the X-Y plane.
- The current I flows in a clockwise direction when viewed from the positive Z-axis.
- A uniform magnetic field →B=B0(^i+√3^j)/2 exists in the region x>(R√3)/2.
2. Determine the Direction of the Magnetic Field:
- The magnetic field can be expressed in terms of its components: Bx=B02 and By=B0√32.
- The angle of the magnetic field with respect to the X-axis can be calculated using tanθ=ByBx=√3, which gives θ=60∘.
3. Calculate the Length Vector:
- The length vector →L for the loop can be expressed as →L=−R^j since the current is flowing clockwise.
4. Using the Force Formula:
- The magnetic force →F on the loop can be calculated using the formula:
→F=I→L×→B
- Substituting the values, we have:
→F=I(−R^j)×(B02^i+B0√32^j)
5. Calculating the Cross Product:
- The cross product can be computed as follows:
→F=I(−R)(^j×(B02^i+B0√32^j))
- This simplifies to:
→F=I(−R)(B02(^j×^i)+B0√32(^j×^j))
- Since ^j×^j=0 and ^j×^i=−^k:
→F=I(−R)(B02(−^k))=IRB02^k
6. Magnitude of the Force:
- The magnitude of the force is:
|→F|=IRB02
7. Relating to Given Expression:
- We know from the problem statement that the magnitude of the magnetic force is given by:
|→F|=B0IRn
- Equating the two expressions:
IRB02=B0IRn
- From this, we can deduce that:
n=2
Final Answer:
The value of n is 2.
- We have a circular wire loop of radius R centered at the origin in the X-Y plane.
- The current I flows in a clockwise direction when viewed from the positive Z-axis.
- A uniform magnetic field →B=B0(^i+√3^j)/2 exists in the region x>(R√3)/2.
- The magnetic field can be expressed in terms of its components: Bx=B02 and By=B0√32.
- The angle of the magnetic field with respect to the X-axis can be calculated using tanθ=ByBx=√3, which gives θ=60∘.
- The length vector →L for the loop can be expressed as →L=−R^j since the current is flowing clockwise.
- The magnetic force →F on the loop can be calculated using the formula:
→F=I→L×→B
- Substituting the values, we have:
→F=I(−R^j)×(B02^i+B0√32^j)
- The cross product can be computed as follows:
→F=I(−R)(^j×(B02^i+B0√32^j))
- This simplifies to:
→F=I(−R)(B02(^j×^i)+B0√32(^j×^j))
- Since ^j×^j=0 and ^j×^i=−^k:
→F=I(−R)(B02(−^k))=IRB02^k
- The magnitude of the force is:
|→F|=IRB02
- We know from the problem statement that the magnitude of the magnetic force is given by:
|→F|=B0IRn
- Equating the two expressions:
IRB02=B0IRn
- From this, we can deduce that:
n=2
The value of n is 2.
Similar Questions
A current carrying circular loop of radius R is placed in a uniform magnetic field B0 Tesla in x-y plane as shown in figure. The loop carries a current i=1A in the direction shown. Find the torqure acting on the loop
View SolutionA circular loop of area 1cm2 carrying a current of 10A is placed in a magnetic field of 2Tˆi. The loop is in xy plane with current in clockwise direction . Fing the torque on the loop
View Solution
Knowledge Check
A circular loop of radius r, carrying a current I lines in y - z plane with its centre at the origin. The net magnetic flux through the loop is
Adirectly proportional to r.BzeroCinversely proportional to r.Ddirectly proportional to I.A circular loop of radius 0.0157 m carriesa current of 2.0 A. The magnetic field at the centre of the loop is
A1.57×10−5Wb/m2B8.0×10−6Wb/m2C2.5×10−5Wb/m2D3.14×10−5Wb/m2A circular loop of radius R carrying current I is kept in XZ plane. A uniform and constant magnetic field →B=(B0ˆi+2B0ˆj+3B0ˆk) exists in the region (B0− a positive constant). Then the magnitude of the torque acting on the loop will be
A2IπR2B0B√5IπR2B0C√10IπR2B0D6IπR2B0
A circular loop of radius 4.0 cm is placed in a horizontal plane and carries an electric current of 5.0 A in the clockwise direction as seen from above. Find the magnetic field (a) at a point 3.0 cm above the centre of the loop (b) at a point 3.0 cm below the centre of the loop.
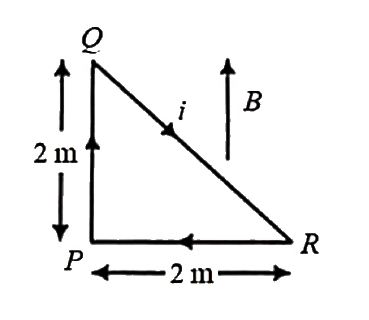
View SolutionA loop PQR carries a current i=2A as shown in the figure. A uniform magnetic field B = 2T exists in space parallel to the plane of the loop . The magnetic torque on the loop is
View SolutionA circular loop of radius R is kept in a uniform magnetic field pointing perpendicular into the plane of paper. When a current l flows in the loop, the tension produced in the loop is

View SolutionA circular wire loop of radius r is placed in a region of uniform magnetic field B such that the plane of the loop makes an angle θ with the direction of B. In which of the following conditions, will no emf be induced in the loop?
View SolutionA conducting circular loop of radiius r carries a constant current i. It is placed in a uniform magnetic field →B0 such that →B0 is perpendicular to the plane of the loop . The magnetic force acting on the loop is
View Solution