Let ABC be a given right isosceles triangle withAB=AC. Sides AB and AC are extended up to E and F, respectively, such that BE×CF=AB2 . Prove that the line EF always passes through a fixed point.
Step by step video & image solution for Let ABC be a given right isosceles triangle with AB = AC. Sides AB and AC are extended up to E and F, respectively, such that BExxCF=AB^(2) . Prove that the line EF always passes through a fixed point. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Let ABC be a given isosceles triangle with AB=AC . Sides ABandAC are extended up to EandF, respectively, such that BExCF=AB2. Prove that the line EF always passes through a fixed point.
View SolutionABC is a triangle in which AB=AC.DandE are points on the sides ABandAC respectively, such that AD=AE. Show that the points B<C<EandD are concyclie.
View Solution
Knowledge Check
In triangle ABC , sides AB and AC are extended to D and E, respectively, such that AB=BD and AC =CE,F∈dDE,ifBC=6 cm.
A3 cmB6cmC9 cmD12 cmIf the equal sides AB and AC (each equal to 5 units) of a right-angled isosceles triangle ABC are produced to P and Q such that BP⋅CQ=AB2, then the line PQ always passes through the fixed point (where A is the origin and AB, AC lie along the positive x and positive y - axis respectively)
A(7,6)B(6,5)C(5,5)D(6,6)In the adjoining figure, ABC is an isosceles triangle in which AB = AC. If E and F be the midpoints of AC and AB respectively, then
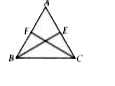 ABE = CFB∠BFC=∠CEBCBF = CEDAll of these
ABE = CFB∠BFC=∠CEBCBF = CEDAll of these
In the given figure, △ABC is an isosceles triangle in which AB - AC. If AB and AC are produced to D and E respectively such that BD = CE, prove that BE = CD. Hint. Show that △ACD=△ABE.
View SolutionIn an isosceles triangle ABC with AB=AC, a circle passing through B and C intersects the sides AB and AC at D and E respectively. Prove that DEBC
View SolutionIn an isosceles triangle ABC with AB=AC, a circle passing through B and C intersects the sides ABandAC atDandE respectively. Prove that DECB.
View SolutionABC is an isosceles triangle in which AB=AC. If D and E are the mid-points of AB and AC respectively, prove that the points B, C, D and E are concyclic.
View SolutionABC is an isosceles triangle in which AB=AC. If DandE are the mid-points of ABandAC respectively, prove that the points B,C,DandE are concylic.
View Solution
