A kettle containing 1kg of water is heated open to atmosphere until evaporation is complete. The work done during this process is
The correct Answer is:172.28
To find the work done during the evaporation of 1 kg of water in an open kettle, we can follow these steps:
Step 1: Understand the Process
When water is heated in an open kettle, it undergoes a phase change from liquid to gas (steam). The work done during this process is primarily due to the expansion of the water vapor against the atmospheric pressure.
Step 2: Identify the Work Done Formula
The work done (W) during the expansion can be expressed as:
W=−PexternalΔV
where ΔV is the change in volume, and Pexternal is the external pressure (atmospheric pressure).
Step 3: Determine the Change in Volume
The change in volume (ΔV) during the evaporation can be approximated as:
ΔV=Vgas−Vliquid
Since the volume of the liquid (water) is much smaller than the volume of the gas (steam), we can simplify this to:
ΔV≈Vgas
Step 4: Use the Ideal Gas Law
For the gas (steam), we can use the ideal gas equation:
PV=nRT
Rearranging gives:
V=nRTP
Thus, the work done can be expressed as:
W=−Pexternal⋅(nRTPexternal)
This simplifies to:
W=−nRT
Step 5: Calculate the Number of Moles (n)
To find n (the number of moles of water), we use the formula:
n=mM
where m is the mass of water (1 kg = 1000 g) and M is the molar mass of water (approximately 18 g/mol):
n=1000g18g/mol≈55.56mol
Step 6: Use the Ideal Gas Constant and Temperature
The ideal gas constant R is approximately 8.314J/(mol K) and the temperature T at which water boils is 373K.
Step 7: Calculate the Work Done
Now we can calculate the work done:
W=−nRT=−(55.56mol)⋅(8.314J/(mol K))⋅(373K)
Calculating this gives:
W≈−173.2kJ
Final Answer
The work done during the evaporation of 1 kg of water is approximately:
W≈−173.2kJ
---
When water is heated in an open kettle, it undergoes a phase change from liquid to gas (steam). The work done during this process is primarily due to the expansion of the water vapor against the atmospheric pressure.
The work done (W) during the expansion can be expressed as:
W=−PexternalΔV
where ΔV is the change in volume, and Pexternal is the external pressure (atmospheric pressure).
The change in volume (ΔV) during the evaporation can be approximated as:
ΔV=Vgas−Vliquid
Since the volume of the liquid (water) is much smaller than the volume of the gas (steam), we can simplify this to:
ΔV≈Vgas
For the gas (steam), we can use the ideal gas equation:
PV=nRT
Rearranging gives:
V=nRTP
Thus, the work done can be expressed as:
W=−Pexternal⋅(nRTPexternal)
This simplifies to:
W=−nRT
To find n (the number of moles of water), we use the formula:
n=mM
where m is the mass of water (1 kg = 1000 g) and M is the molar mass of water (approximately 18 g/mol):
n=1000g18g/mol≈55.56mol
The ideal gas constant R is approximately 8.314J/(mol K) and the temperature T at which water boils is 373K.
Now we can calculate the work done:
W=−nRT=−(55.56mol)⋅(8.314J/(mol K))⋅(373K)
W≈−173.2kJ
The work done during the evaporation of 1 kg of water is approximately:
W≈−173.2kJ
Similar Questions
Knowledge Check
- Question 1 - Select One
An ideal gas system undergoes an isothermal process, then the work done during the process is
AnRTln(V2V1)BnRTln(V1V2)C2nRTln(V2V1)D2nRTln(V1V2) - Question 2 - Select One
An ideal gas system undergoes an isothermal process, then the work done during the process is
AnRTInV2V1BnRTInV1V2C2nRTInV2V1D2nRTInV1V2 - Question 3 - Select One
Figure shows a hollow cube of side 'a' and volume 'V'. There is a small chamber of volume V/4 in the cube as shown. The chamber is completely filled by in kg of water. Water leaks through a hole H and spreads in the whole cube. Then the work done by gravity in this process assuming that the complete water finally lies at the bottom of the cube is
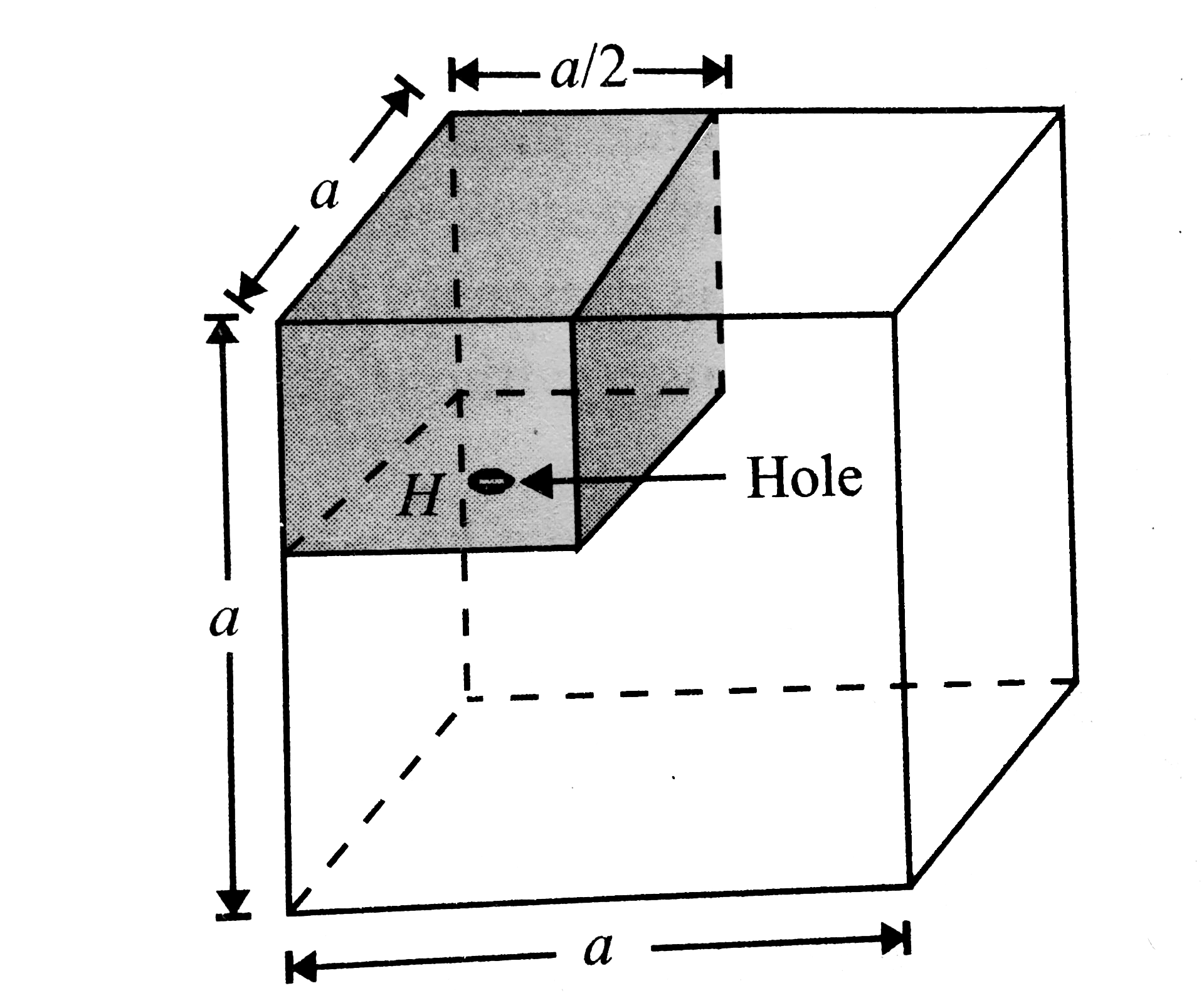 A12mgaB38mgaC58mgaD18mga
A12mgaB38mgaC58mgaD18mga
Define adiabatic process. Derive an expression for work done during adiabatic process.
View SolutionA cyclic process is shown in the figure. Work done during the cyclic process ABCDA is
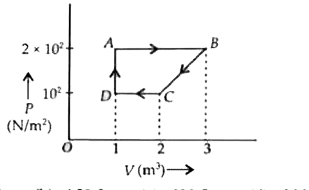 View Solution
View SolutionA cyclic process is shown in the figure. Work done during the cyclic process ABCDA is
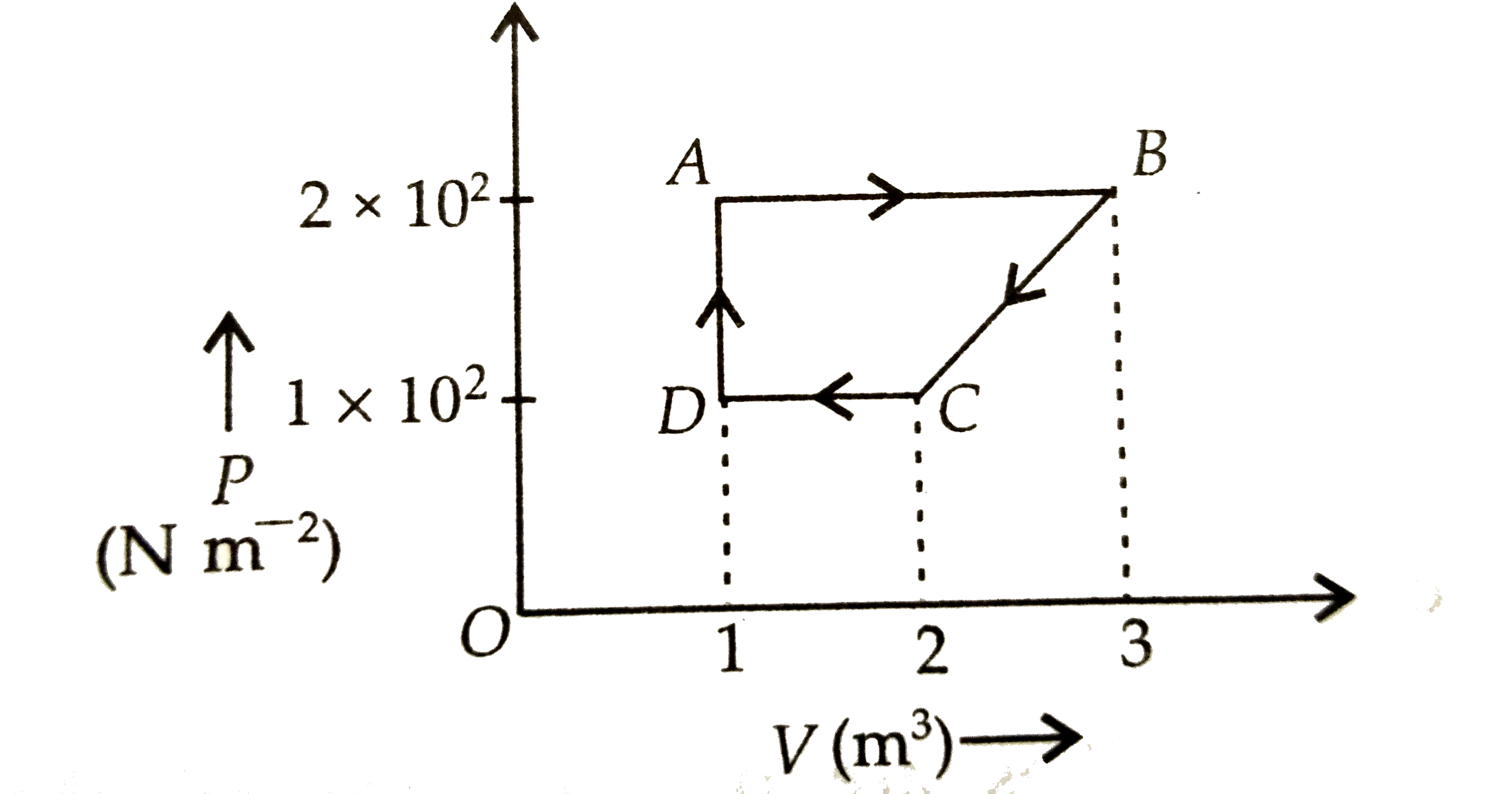 View Solution
View SolutionFind out work done by the battery during he process of charging
View SolutionThe change in internal energy of two moles of a gas during adiabatic expansion is found to be -100 Joule. The work done during the process is
View Solution

