An X-ray of lower abdomen shown a shadow in the region of the ureter suspected to be a uretelic calculus. A possible clinical symptom would be
Active renal failure
Anuria and haematuria
Motor aphasia
Chronic renal failure (CRF)
The correct Answer is:B
Step by step video, text & image solution for An X-ray of lower abdomen shown a shadow in the region of the ureter suspected to be a uretelic calculus. A possible clinical symptom would be by Biology experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - DINESH PUBLICATIONCHAPTER - EXCRETORY PRODUCTS AND THEIR ELIMINATIONEXERCISE - Check your graps10videos
EXCRETORY PRODUCTS AND THEIR ELIMINATION
- BOOK - DINESH PUBLICATIONCHAPTER - EXCRETORY PRODUCTS AND THEIR ELIMINATIONEXERCISE - Check your graps10videos
EXCRETORY PRODUCTS AND THEIR ELIMINATION
- BOOK - DINESH PUBLICATIONCHAPTER - EVIDENCES OF EVOLUTIONEXERCISE - CHECK YOUR GRASP3videos
EVIDENCES OF EVOLUTION
- BOOK - DINESH PUBLICATIONCHAPTER - FAMILIES OF FLOWERING PLANTSEXERCISE - BRAIN TEASERS -II97videos
FAMILIES OF FLOWERING PLANTS
Similar Questions
An X-ray of the lower abdomen shows a shadow in the region of the ureter suspected to be a ureteric calculus. A possible clinical symptom would be
View SolutionAnswer the following question:
(a) Long distance radio broadcasts use short wave bands. Why?
(b) It is necessary to use satallites for long distance T.V. Transmission. Why?
(c) Optical and radio telescope are built on the ground but X-ray astronomy is possible only from satellites orbiting the earth. Why?
(d) The small ozone layer on top of the atmosphere is crucial for human survival. Why?
(e) If the earth did not have atmosphere, would its average surface temperature be higher or lower than what it is now?
(f) Some scientists have predicted that a global nuclear war on the earth would be followed by a severe 'nuclear winter' with a devastating effect on life on earth. What might be the basis of this prediction.View Solution
Knowledge Check
- Question 1 - Select One
After the faliure of Bohr atomic theory but its ability to explain to the atomic spectral a need was felt for the new model that could incorporate, the concept of stationary orbit, de Broglie concept, Heisenberg uncertainity principle. The concept that in corporate above facts is called quantum mechanics of the atomic model wave mchanical model. it includes set of quantum number and ∣∣ψ2∣∣ a mathematical expression of the probability of finding an electron at all points in space. This probability function is the best indication available of how the electon behaves, for as a consequence of the Uncertainity Principle, the amount we can know about the electron is limited. While quantum mechanics can tell us the exact probability of finding an electron at any two particular points, it does not tell us how the electron moves from one of these points to the other. Thus the idea of an electron orbit is lost, it is replaced with a description of where the electron is most likely to be found. This total picture of the probability of finding an electron at various points in space is called an orbital.
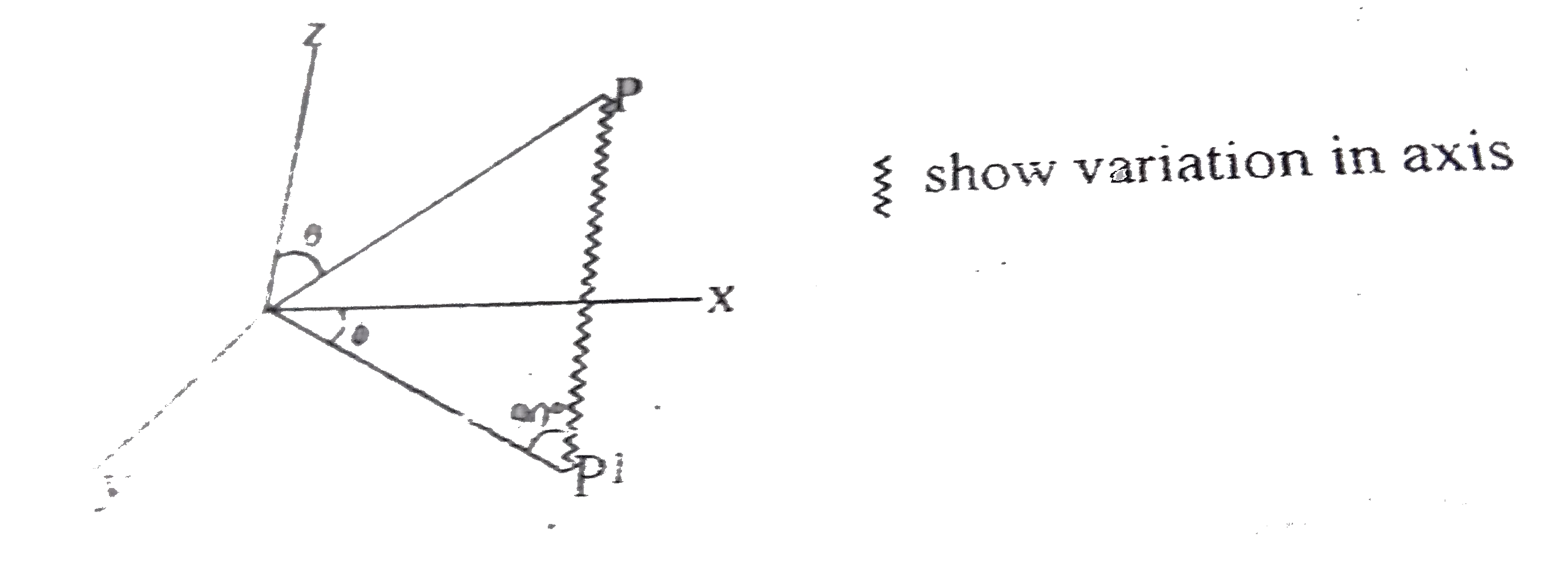
There are various types of orbitals possible, each corresponding to one of the possible combinations of quantum numbers. These orbitals are classified according to the value of n and l associated with them. In order to avoid confusion over the use of two numbers, the numerical velues of l are replaced by letters, electrons in orbitals with l=0 are called s-electrons those occupying orbitals for which l=1 are p-electrons and those for which l=2 are called d-electrons. The numerical and alphabetical correspondences are summarized in table. Using the alphabetical notation for l, we would say that in the ground state of hydrogen atom (n=1,l=0) we have a 1s-electron, or that the electron moves in a 1s-orbital. The relation of the spherical polar co-ordinates r,θ and ϕ to Cartesian coordinates x, y and z. To make the concept of an orbital more meaningful, it is helpful to examine the actual solution of the wave function for the one-electron atom. Because of the spherical sysmmetry of the atom, the wave functions are most simply expressed in terms of a spherical polar-coordinate system, shown in fig., which has its orbit at the nucleus. It is found that the wave function can be expressed as the product of two functions, one of which (the ''angular part'' X) depends only the angle θ and ϕ the other of which (the ''radial part'' R) depends only on the distance from the nucleus. Thus we have
ϕ(r,θ,ϕ)=R(r)X(θ,ϕ)
Angular and radial parts of hydrogen atom wave function
(Angular partX(θ,ϕ),,Radial partRn,l(r)),(X(s)=(14π)1/2,,R(1s)=2(za0)3/2e−σ/2),(X(px)=(34π)1/2sinθcosϕ,,R(2s)=12√2(za0)3/2(2−σ)e−σ/2),(X(py)=(34π)1/2sinθsinϕ,,R(2p)=12√6(za0)3/2σe−σ/2),(X(pz)=(34π)1/2cosθ,,),(X(d22)=(516π)1/2(3cos2θ−1),,),(X(dxz)=(154π)1/2sinθcosθcosϕ,,R(3s)=19√3(za0)3/2(6−6σ+σ2)e−σ/2),(X(dyz)=(154π)1/2sinθcosθsinϕ,,R(3p)=19√6(za0)3/2(4−σ)σe−σ/2),(X(dx2−y2)=(154π)1/2sin2θcos2ϕ,,R(3d)=19√30(za0)3/2σ2e−σ/2),(X(dxy)=(154π)1/2sin2θsin2ϕ,,),(,,σ=2Zrna0,a0=h24π2me2)
This factrorization helps us to visualize the wave function, since it allows us to consider the angular and radial dependences separately. It contains the expression for the angular and radial parts of the one electron atom wave function. Note that the angular part of the wave function for an s-orbital it alwats the same, (1/4π)1/2 regardless of principal quantum number. It is also true that the angular dependence of the p-orbitals and of the d-orbitals is independent of principle quantum number. Thus all orbitals of given types (s, p, or d) have the same angular behavour The table shows, however, that the radial part of the wave function depends both on the principal quantum n and on the angular momentum quantum number l.
To find the wave function for a particular state, we simply multiply the appropriate angular and radial parts togather called normalized wave function.
The probability of finding an electron at a point within an atom is proportional to the square of orbital wave function, i.e., ψ2 at that point. Thus, ψ2 is known as probability density and always a positive quantity.
ψ2dV(orψ2.4πr2dr). represents the probability for finding electron in a small volume dV surrounding the nucleus.
The electron probility density for 1s-orbital best represented by the relation.A12√π(Za0)3/2×era0B1π(Za0)3×e−2zra0C1π(Za0)3/2×era0D2π(Za0)3×e−2zra0 - Question 2 - Select One
After the faliure of Bohr atomic theory but its ability to explain to the atomic spectral a need was felt for the new model that could incorporate, the concept of stationary orbit, de Broglie concept, Heisenberg uncertainity principle. The concept that in corporate above facts is called quantum mechanics of the atomic model wave mchanical model. it includes set of quantum number and ∣∣ψ2∣∣ a mathematical expression of the probability of finding an electron at all points in space. This probability function is the best indication available of how the electon behaves, for as a consequence of the Uncertainity Principle, the amount we can know about the electron is limited. While quantum mechanics can tell us the exact probability of finding an electron at any two particular points, it does not tell us how the electron moves from one of these points to the other. Thus the idea of an electron orbit is lost, it is replaced with a description of where the electron is most likely to be found. This total picture of the probability of finding an electron at various points in space is called an orbital.
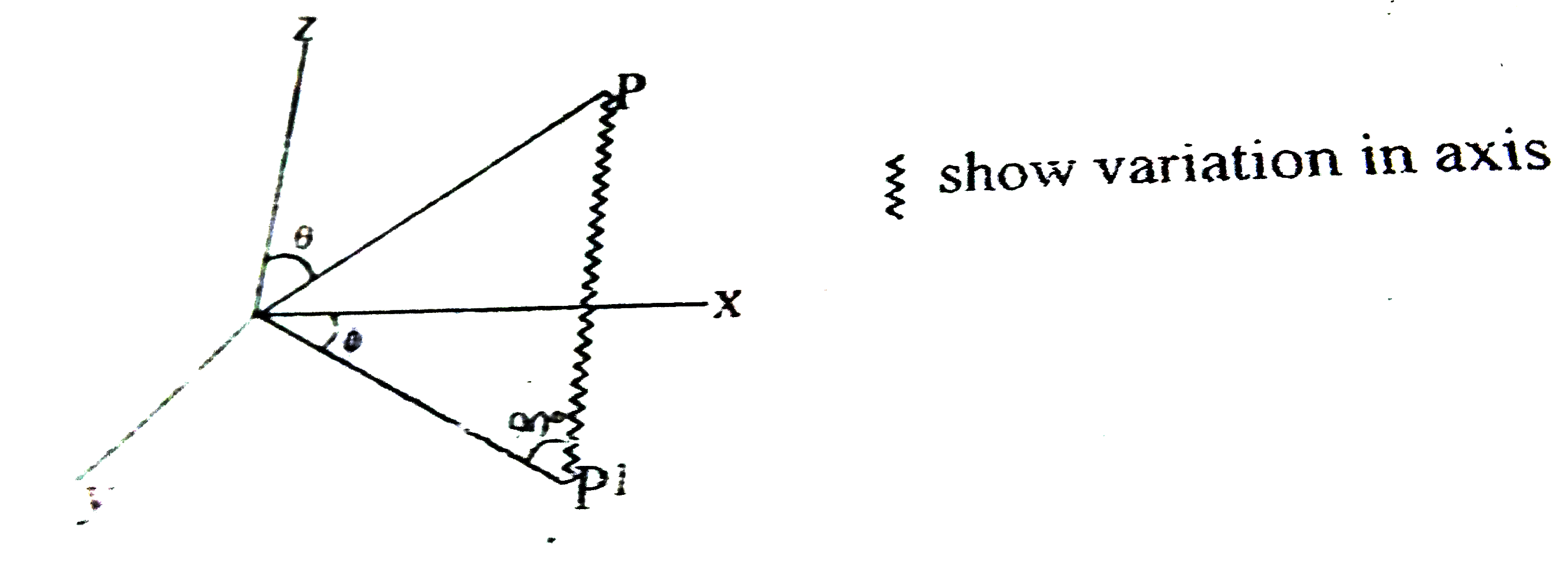
There are various types of orbitals possible, each corresponding to one of the possible combinations of quantum numbers. These orbitals are classified according to the value of n and l associated with them. In order to avoid confusion over the use of two numbers, the numerical velues of l are replaced by letters, electrons in orbitals with l=0 are called s-electrons those occupying orbitals for which l=1 are p-electrons and those for which l=2 are called d-electrons. The numerical and alphabetical correspondences are summarized in table. Using the alphabetical notation for l, we would say that in the ground state of hydrogen atom (n=1,l=0) we have a 1s-electron, or that the electron moves in a 1s-orbital. The relation of the spherical polar co-ordinates r,θ and ϕ to Cartesian coordinates x, y and z. To make the concept of an orbital more meaningful, it is helpful to examine the actual solution of the wave function for the one-electron atom. Because of the spherical sysmmetry of the atom, the wave functions are most simply expressed in terms of a spherical polar-coordinate system, shown in fig., which has its orbit at the nucleus. It is found that the wave function can be expressed as the product of two functions, one of which (the ''angular part'' X) depends only the angle θ and ϕ the other of which (the ''radial part'' R) depends only on the distance from the nucleus. Thus we have
ϕ(r,θ,ϕ)=R(r)X(θ,ϕ)
Angular and radial parts of hydrogen atom wave function
(Angular partX(θ,ϕ),,Radial partRn,l(r)),(X(s)=(14π)1/2,,R(1s)=2(za0)3/2e−σ/2),(X(px)=(34π)1/2sinθcosϕ,,R(2s)=12√2(za0)3/2(2−σ)e−σ/2),(X(py)=(34π)1/2sinθsinϕ,,R(2p)=12√6(za0)3/2σe−σ/2),(X(pz)=(34π)1/2cosθ,,),(X(d22)=(516π)1/2(3cos2θ−1),,),(X(dxz)=(154π)1/2sinθcosθcosϕ,,R(3s)=19√3(za0)3/2(6−6σ+σ2)e−σ/2),(X(dyz)=(154π)1/2sinθcosθsinϕ,,R(3p)=19√6(za0)3/2(4−σ)σe−σ/2),(X(dx2−y2)=(154π)1/2sin2θcos2ϕ,,R(3d)=19√30(za0)3/2σ2e−σ/2),(X(dxy)=(154π)1/2sin2θsin2ϕ,,),(,,σ=2Zrna0,a0=h24π2me2)
This factrorization helps us to visualize the wave function, since it allows us to consider the angular and radial dependences separately. It contains the expression for the angular and radial parts of the one electron atom wave function. Note that the angular part of the wave function for an s-orbital it alwats the same, (1/4π)1/2 regardless of principal quantum number. It is also true that the angular dependence of the p-orbitals and of the d-orbitals is independent of principle quantum number. Thus all orbitals of given types (s, p, or d) have the same angular behavour The table shows, however, that the radial part of the wave function depends both on the principal quantum n and on the angular momentum quantum number l.
To find the wave function for a particular state, we simply multiply the appropriate angular and radial parts togather called normalized wave function.
The probability of finding an electron at a point within an atom is proportional to the square of orbital wave function, i.e., ψ2 at that point. Thus, ψ2 is known as probability density and always a positive quantity.
ψ2dV(orψ2.4πr2dr). represents the probability for finding electron in a small volume dV surrounding the nucleus.
The angular wave function of which orbital with not disturb by the variation with azimuthal angle onlyA1s and 2sB2pz and 2d2zC2px and 3d2zD2px and 2s - Question 3 - Select One
The properties of x -rays as put forwarded by Rontgen in his pioneering paper on the topic are as follos:
X-rays posses a very strong pentrative power it can penetrate wood upto 3cm and and aluminium foil upto 15mm . If the hand if the hand is held between the discharge tube and the screen the dark shadow of the of the bones os visible within the slightly dark shadow of the hand"
photographc plates and film "show themselves susceptible to x- rays " Hence , photography provided a valuable method of studying the effect of x-rays
xrays neither reflected nor reflected refracted (so far as Rontgen could discover ). Hence , " X - rays as cannot be concerted by lenses"
X- rays discharge electrified bodies , whether the electrification is positive or negative .
X-rays are generated when the cathode rays of the discharge tube strike any solid body .A heavier element , such as plantium , however is much more efficient as a generator of X - rays than a lighter element , such as aluminium . Most of Rontgen 's observation stood the test of time, though some of them needed to be modified later. V, then maximum energy of emitted photon could be Emax=eV,hcλmin=hceV
λmin is also called cut off wavelength . since electron may loose very small energy in a given collision, the upper value of lambd eill approach infinity . when X-rays is produced in X-ray tube , two types of X-rays spectra and line are observed: continous spectra and line spectra. A continous spectra is produced by bremsstrahlung, the electromagnetic radiation produced when free electron are accelerated during collision with ions.
A line spectrum result when an electra having sufficient energy collides with a heavy atom, and an electr in an inner energy level is ejected from the atom . An electra from an outer energy level then fills the vacant inner energy level, resulting in emission of an X-ray photon.
 The electron knocks out an inner shell electron of the atom with which it collides . Let us take an hypothetical case of a target atom whose K- shell electron has been knocked out as shown.
The electron knocks out an inner shell electron of the atom with which it collides . Let us take an hypothetical case of a target atom whose K- shell electron has been knocked out as shown. 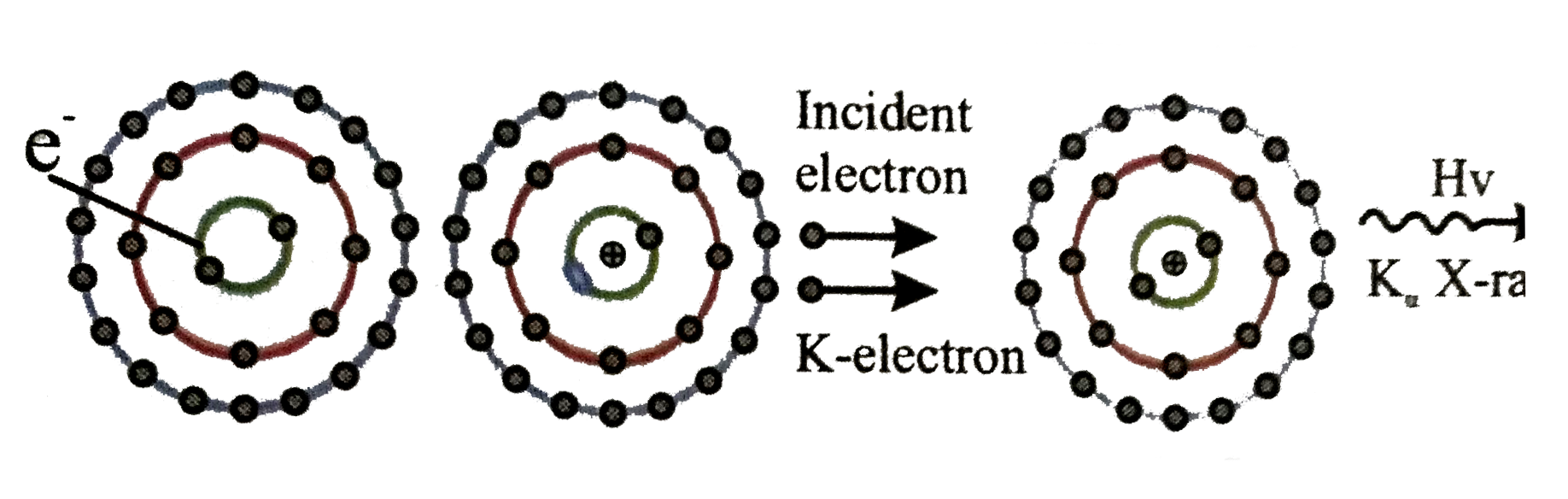 this will create a vacancy in K-shell . sensing this vacancy an electron from a higher energy state may make a trasition to thsi vacant state. when such a transition take placce the differece of energy is converted into photon of electromagnetic radiation, which is called charactertistic X-rays . Now depending upon the shell from which an electron make a trasition to K -shell we may have different lines in the K series of Xrays e.g. if electron from L shell jumps to K shell we have K_(alpha), if electron from M shell jumps to K shell we have Kβ X -rays and so . on . Monseley conducted many experiment on characteristic X-rays , the finding of whcih played an inportant role in . developing the concept opf atomic number . Moseley's observation can be expressed as √v=a(Z−b)
this will create a vacancy in K-shell . sensing this vacancy an electron from a higher energy state may make a trasition to thsi vacant state. when such a transition take placce the differece of energy is converted into photon of electromagnetic radiation, which is called charactertistic X-rays . Now depending upon the shell from which an electron make a trasition to K -shell we may have different lines in the K series of Xrays e.g. if electron from L shell jumps to K shell we have K_(alpha), if electron from M shell jumps to K shell we have Kβ X -rays and so . on . Monseley conducted many experiment on characteristic X-rays , the finding of whcih played an inportant role in . developing the concept opf atomic number . Moseley's observation can be expressed as √v=a(Z−b)
where a and b are constants. Z is the atomic number of target atom n is the frequency .
A (##NAR_PHY_XII_V05_C02_E01_312_O01.png" width="30%">B (##NAR_PHY_XII_V05_C02_E01_312_O02.png" width="30%">C (##NAR_PHY_XII_V05_C02_E01_312_O03.png" width="30%">D (##NAR_PHY_XII_V05_C02_E01_312_O04.png" width="30%">
Answer the following questions: (a) Long distance radio broadcasts use short-wave bands. Why? (b) It is necessary to use satellites for long distance TV transmission. Why? (c) Optical and radiotelescopes are built on the ground but X-ray astronomy is possible only from satellites orbiting the earth. Why? (d) The small ozone layer on top of the stratosphere is crucial for human survival. Why? (e) If the earth did not have an atmosphere, would its average surface temperature be higher or lower than what it is now? (f) Some scientists have predicted that a global nuclear war on the earth would be followed by a severe ‘nuclear winter’ with a devastating effect on life on earth. What might be the basis of this prediction? Answer the following questions: (a) Long distance radio broadcasts use short-wave bands. Why? (b) It is necessary to use satellites for long distance TV transmission. Why? (c) Optical and radiotelescopes are built on the ground but X-ray astronomy is possible only from satellites orbiting the earth. Why? (d) The small ozone layer on top of the stratosphere is crucial for human survival. Why? (e) If the earth did not have an atmosphere, would its average surface temperature be higher or lower than what it is now? (f) Some scientists have predicted that a global nuclear war on the earth would be followed by a severe ‘nuclear winter’ with a devastating effect on life on earth. What might be the basis of this prediction?
View SolutionFor the potentiometer circuit shown in the given figure, points X and Y represent the two terminals of an unknown emf ε . A student observed that when the jockey is moved from the end A to the end B of the potentiometer wire, the direction of the deflection in the galvanometer remains in the same direction. What may be the two possible faults in the circuit that could result in this observations ? If the galvanometer deflection at the end B is (i) more, (ii) less, than that at the end A which of the two faults," listed above, would be there in the circuit ? Give reasons in support of your answer in each case.
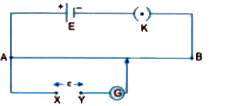 View Solution
View SolutionThe properties of x -rays as put forwarded by Rontgen in his pioneering paper on the topic are as follos:
X-rays posses a very strong pentrative power it can penetrate wood upto 3cm and and aluminium foil upto 15mm . If the hand if the hand is held between the discharge tube and the screen the dark shadow of the of the bones os visible within the slightly dark shadow of the hand"
photographc plates and film "show themselves susceptible to x- rays " Hence , photography provided a valuable method of studying the effect of x-rays
xrays neither reflected nor reflected refracted (so far as Rontgen could discover ). Hence , " X - rays as cannot be concerted by lenses"
X- rays discharge electrified bodies , whether the electrification is positive or negative .
X-rays are generated when the cathode rays of the discharge tube strike any solid body .A heavier element , such as plantium , however is much more efficient as a generator of X - rays than a lighter element , such as aluminium . Most of Rontgen 's observation stood the test of time, though some of them needed to be modified later. V, then maximum energy of emitted photon could be Emax=eV,hcλmin=hceV
λmin is also called cut off wavelength . since electron may loose very small energy in a given collision, the upper value of lambd eill approach infinity . when X-rays is produced in X-ray tube , two types of X-rays spectra and line are observed: continous spectra and line spectra. A continous spectra is produced by bremsstrahlung, the electromagnetic radiation produced when free electron are accelerated during collision with ions.
A line spectrum result when an electra having sufficient energy collides with a heavy atom, and an electr in an inner energy level is ejected from the atom . An electra from an outer energy level then fills the vacant inner energy level, resulting in emission of an X-ray photon.
 The electron knocks out an inner shell electron of the atom with which it collides . Let us take an hypothetical case of a target atom whose K- shell electron has been knocked out as shown.
The electron knocks out an inner shell electron of the atom with which it collides . Let us take an hypothetical case of a target atom whose K- shell electron has been knocked out as shown. 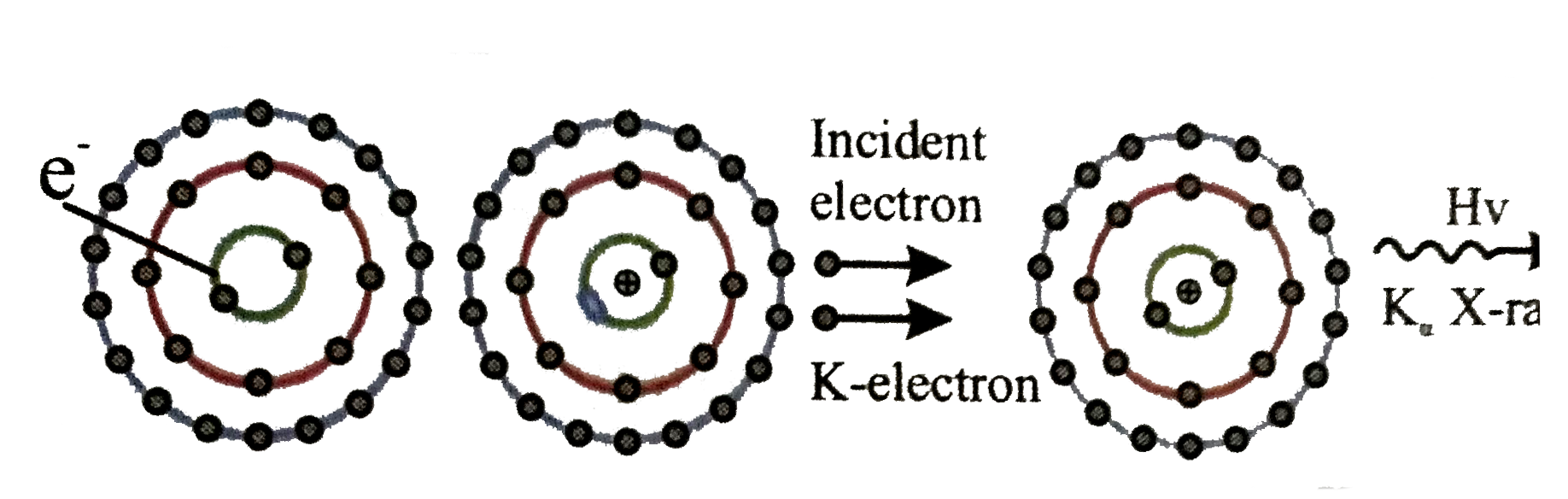 this will create a vacancy in K-shell . sensing this vacancy an electron from a higher energy state may make a trasition to thsi vacant state. when such a transition take placce the differece of energy is converted into photon of electromagnetic radiation, which is called charactertistic X-rays . Now depending upon the shell from which an electron make a trasition to K -shell we may have different lines in the K series of Xrays e.g. if electron from L shell jumps to K shell we have K_(alpha), if electron from M shell jumps to K shell we have Kβ X -rays and so . on . Monseley conducted many experiment on characteristic X-rays , the finding of whcih played an inportant role in . developing the concept opf atomic number . Moseley's observation can be expressed as √v=a(Z−b)
this will create a vacancy in K-shell . sensing this vacancy an electron from a higher energy state may make a trasition to thsi vacant state. when such a transition take placce the differece of energy is converted into photon of electromagnetic radiation, which is called charactertistic X-rays . Now depending upon the shell from which an electron make a trasition to K -shell we may have different lines in the K series of Xrays e.g. if electron from L shell jumps to K shell we have K_(alpha), if electron from M shell jumps to K shell we have Kβ X -rays and so . on . Monseley conducted many experiment on characteristic X-rays , the finding of whcih played an inportant role in . developing the concept opf atomic number . Moseley's observation can be expressed as √v=a(Z−b)
where a and b are constants. Z is the atomic number of target atom n is the frequency .
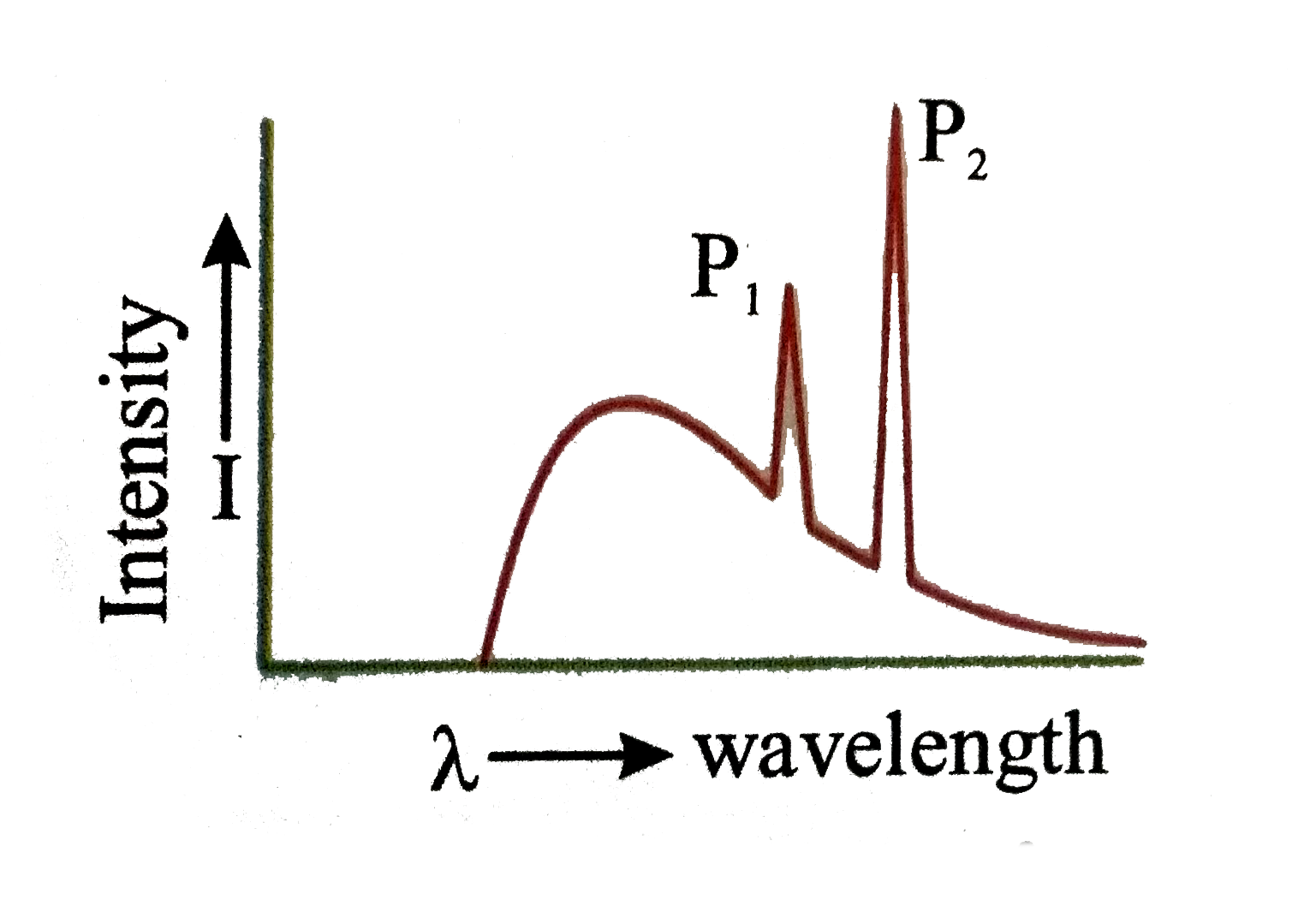
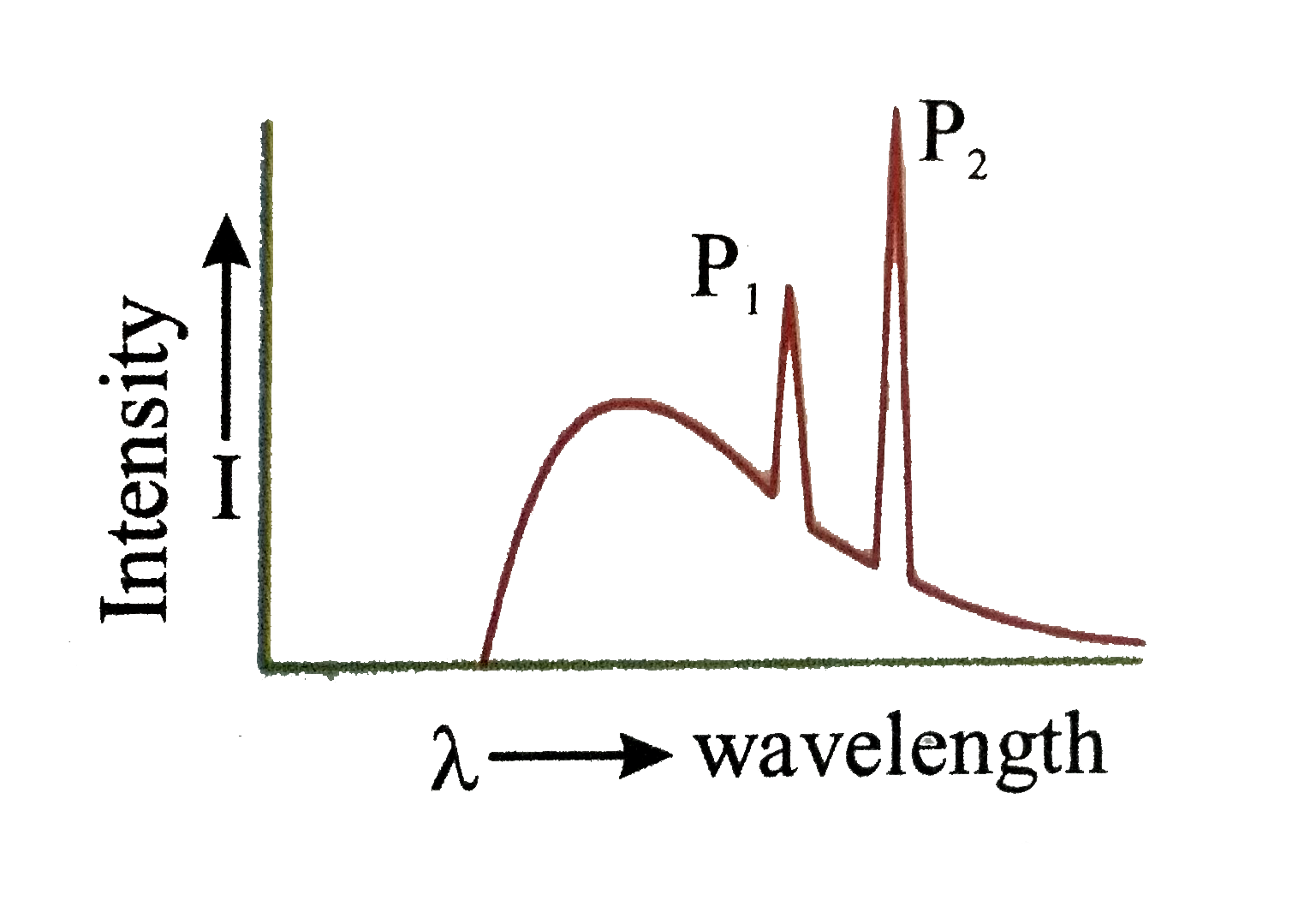
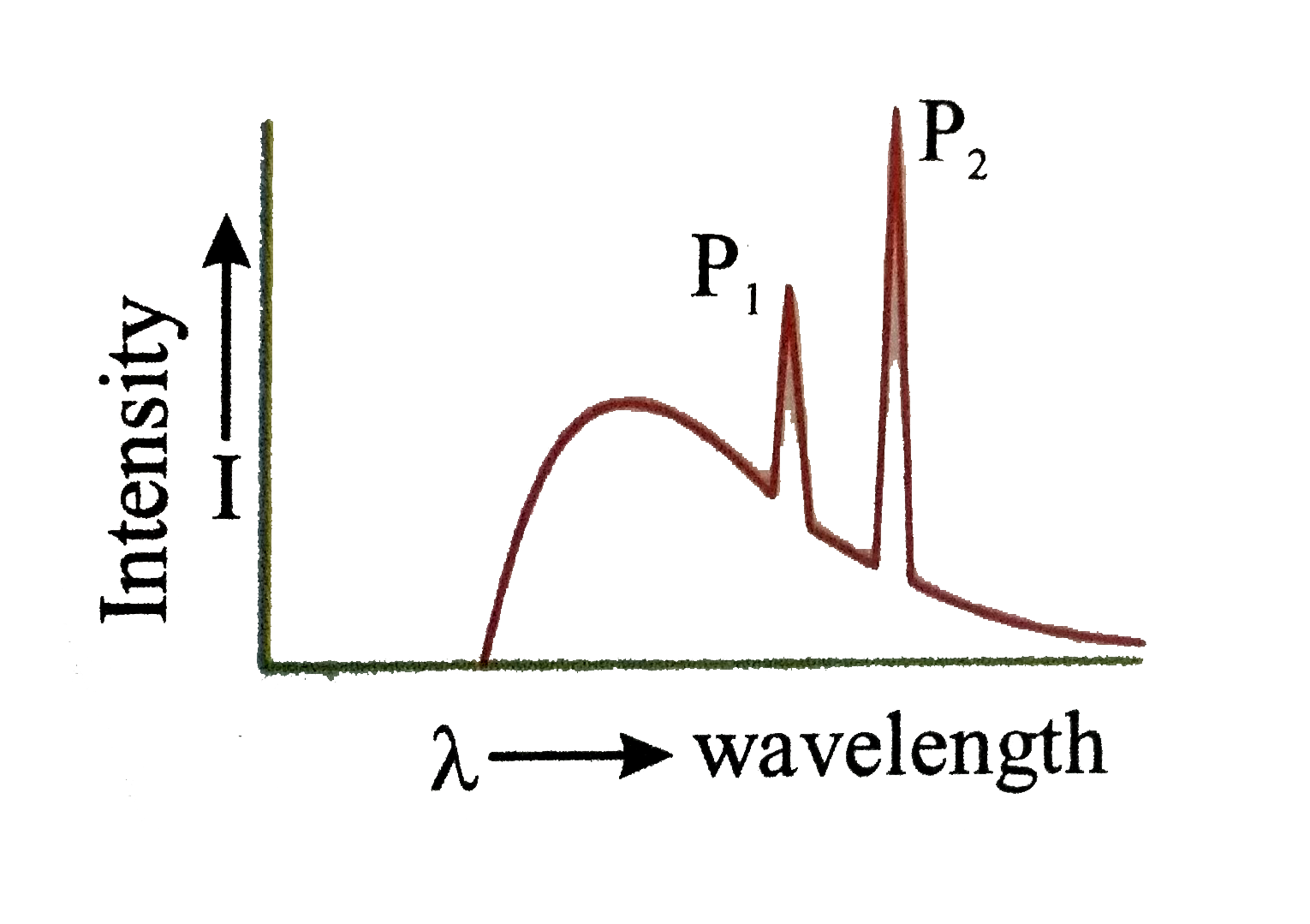
In intensity V//s wavelength graph, which of the following process is reponsible for the intensity of peaks p1 and p2?View SolutionThe properties of x -rays as put forwarded by Rontgen in his pioneering paper on the topic are as follos:
X-rays posses a very strong pentrative power it can penetrate wood upto 3cm and and aluminium foil upto 15mm . If the hand if the hand is held between the discharge tube and the screen the dark shadow of the of the bones os visible within the slightly dark shadow of the hand"
photographc plates and film "show themselves susceptible to x- rays " Hence , photography provided a valuable method of studying the effect of x-rays
xrays neither reflected nor reflected refracted (so far as Rontgen could discover ). Hence , " X - rays as cannot be concerted by lenses"
X- rays discharge electrified bodies , whether the electrification is positive or negative .
X-rays are generated when the cathode rays of the discharge tube strike any solid body .A heavier element , such as plantium , however is much more efficient as a generator of X - rays than a lighter element , such as aluminium . Most of Rontgen 's observation stood the test of time, though some of them needed to be modified later. V, then maximum energy of emitted photon could be Emax=eV,hcλmin=hceV
λmin is also called cut off wavelength . since electron may loose very small energy in a given collision, the upper value of lambd eill approach infinity . when X-rays is produced in X-ray tube , two types of X-rays spectra and line are observed: continous spectra and line spectra. A continous spectra is produced by bremsstrahlung, the electromagnetic radiation produced when free electron are accelerated during collision with ions.
A line spectrum result when an electra having sufficient energy collides with a heavy atom, and an electr in an inner energy level is ejected from the atom . An electra from an outer energy level then fills the vacant inner energy level, resulting in emission of an X-ray photon.
 The electron knocks out an inner shell electron of the atom with which it collides . Let us take an hypothetical case of a target atom whose K- shell electron has been knocked out as shown.
The electron knocks out an inner shell electron of the atom with which it collides . Let us take an hypothetical case of a target atom whose K- shell electron has been knocked out as shown. 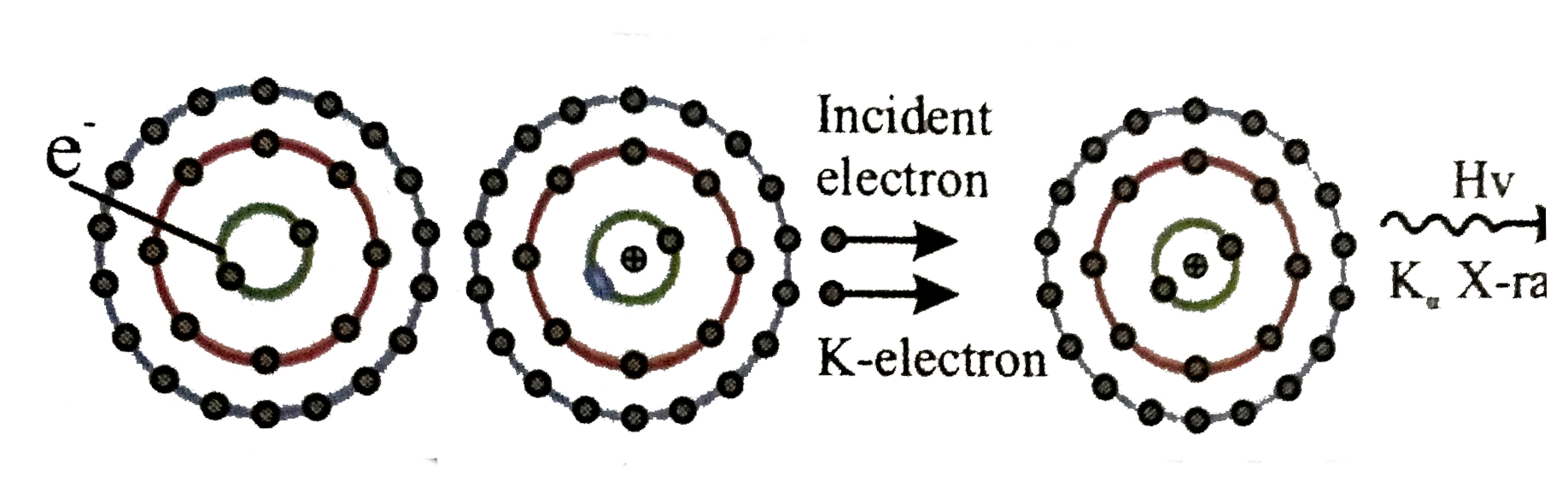 this will create a vacancy in K-shell . sensing this vacancy an electron from a higher energy state may make a trasition to thsi vacant state. when such a transition take placce the differece of energy is converted into photon of electromagnetic radiation, which is called charactertistic X-rays . Now depending upon the shell from which an electron make a trasition to K -shell we may have different lines in the K series of Xrays e.g. if electron from L shell jumps to K shell we have K_(alpha), if electron from M shell jumps to K shell we have Kβ X -rays and so . on . Monseley conducted many experiment on characteristic X-rays , the finding of whcih played an inportant role in . developing the concept opf atomic number . Moseley's observation can be expressed as √v=a(Z−b)
this will create a vacancy in K-shell . sensing this vacancy an electron from a higher energy state may make a trasition to thsi vacant state. when such a transition take placce the differece of energy is converted into photon of electromagnetic radiation, which is called charactertistic X-rays . Now depending upon the shell from which an electron make a trasition to K -shell we may have different lines in the K series of Xrays e.g. if electron from L shell jumps to K shell we have K_(alpha), if electron from M shell jumps to K shell we have Kβ X -rays and so . on . Monseley conducted many experiment on characteristic X-rays , the finding of whcih played an inportant role in . developing the concept opf atomic number . Moseley's observation can be expressed as √v=a(Z−b)
where a and b are constants. Z is the atomic number of target atom n is the frequency .
X-rays of high penetratrating power are called hard X-ray. Hard X-rays have energy of the order of 105eV. the minimum potential differece through ehich the electron should be accelerated in an X-ray tube to obtain X-ray of energy 105eV is:View SolutionVarious rules of thumb have seen proposed by the scientific community to expalin the mode of radioactive decay by various radioisotopes. One of the major rules is called the n/p ratio. If all the known isotopes of the elemnts are plotted on a graph of number of neutrons (n) versus number of protons (p), it is observed that all isotopes lying outside of a ''stable'' n/p ratio region are radioactive as shown fig. The graph exhibits straight line behaviour with unit slope up to p=25. Above p=25, tgose isotopes with n/p ratios lying above the stable region usually undergo beta decay. Very heavy isotopes (p>83) are unstable because of their relativley large nuclei and they undergo alpha decay. Gamma ray emission does not involve the release of a particle. It represnts a change in an atom from a higher energy level to a lower energy level.
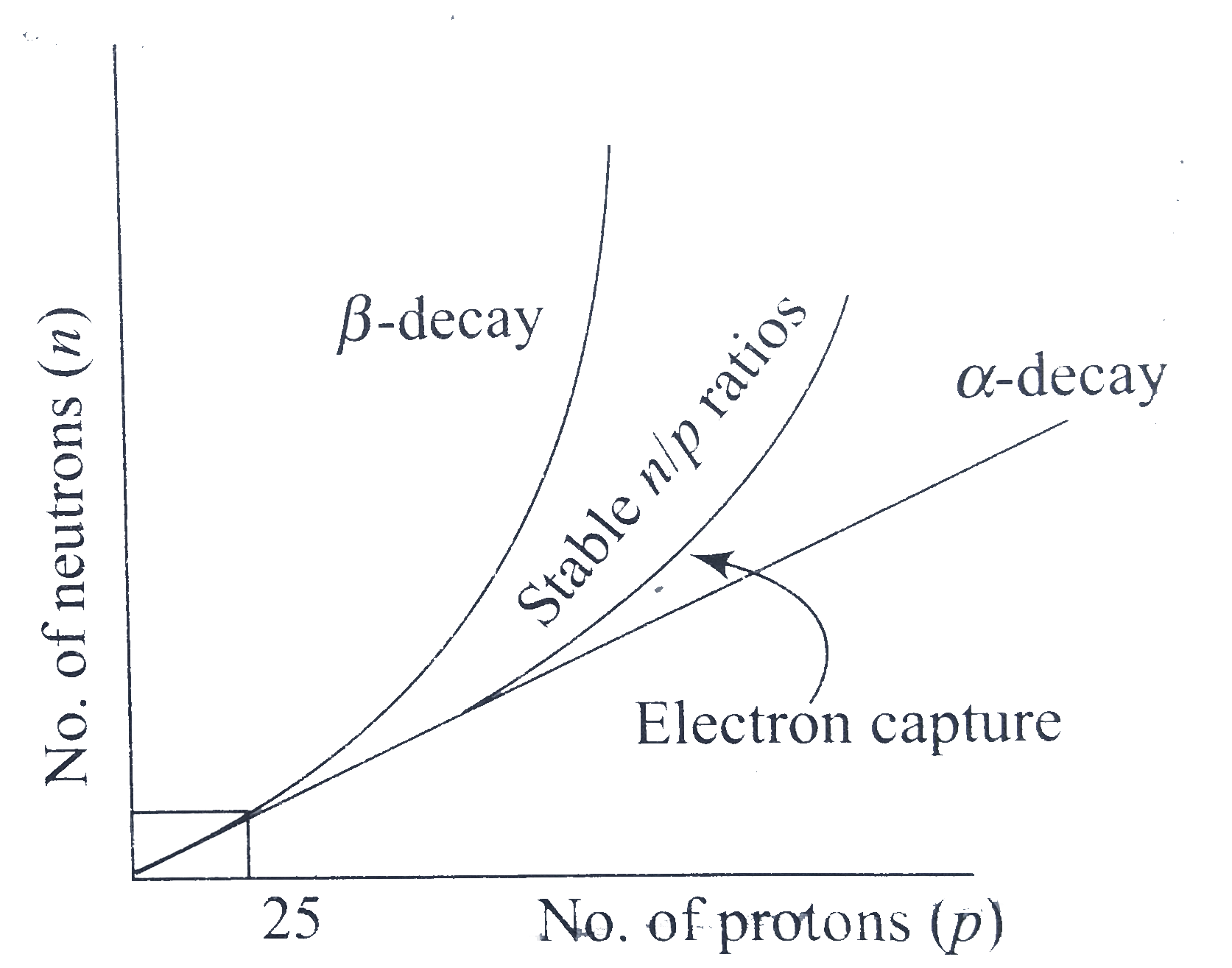
How would the radioisotope of magnesium with atomic mass 27 undergo radioactive decay?.View Solution

