According to de-Brogile, matter should exhibit dual behaviour, that is both particle and wave like properties. However, a cricket ball of mass 100 g does not move like a wave when it is thrown by a b owler at a speed of 100km/h. calculate the wavelength of the ball and explain why it does not show wave nature.
Given,
From de-Brogile equation , wavelength
As the wavelength is very small so wave nature cannot be deteched.
Topper's Solved these Questions
Similar Questions
According to de-Brogile, matter should exhibit dual behaviour, that is both particle and wave like properties. However, a cricket ball of mass 100 g does not move like a wave when it is thrown by a b owler at a speed of 100km/h. calculate the wavelength of the ball and explain why it does not show wave nature.
View SolutionA tennis ball of mass 6.0x10−2kg is moving with a speed of 62ms−1 . Calculate the wavelength associated with this moving tennis ball. Will the movement of this ball exhibit a wave character?
View Solution
Knowledge Check
According to de-Broglie, matter should exhibit dual behviour, that is both particle and wave like properties. Calculate the wavelength of a cricket ball of mass 100 g when it is thrown by a bowler at a speed of 100km/h.
A2.385×10−38mB23.85×10−36mC238.5×10−38mD238×10−36mMacroscopic objects like a moving cricket ball does not show any wave like properties because
Ade broglie hypothesis is not trueBde broglie hypothesis is true only for electronsCde broglie hypothesis is true only for photonsDwavelength associated with a macroscopic object is smallDe-Broglie hypothesized that material particles have wave like properties. Figure shows a small particle in a box. The particle simply bounces back and forth at constant speed. As particles also have wave like properties it can be considered to be a wave reflecting back and forth from the ends of the box. The reflections will create a standing wave analogous to standing wave on a string tied at both ends. Since a standing wave confined to a region can have only selected wavelength, momentum of the particle is quantized. We can safely assume that such a particle only has kinetic energy. This energy must also be quantized.
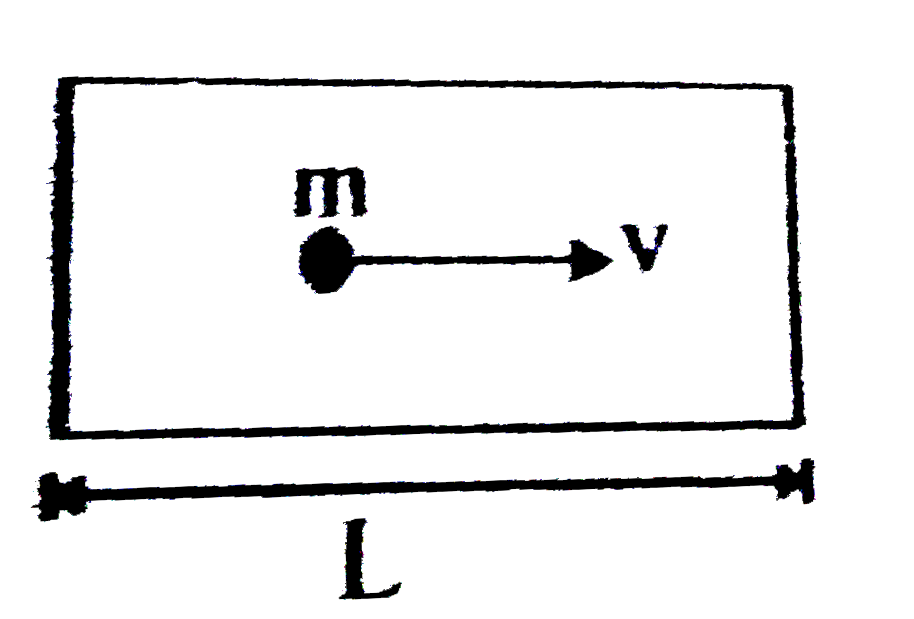
What is momentum of particle in n^(th) mode of standing wave ?Anh2LBnhLC2nhLD2Lnh
wavelength of Bullet. Calculate the de-Brogli wavelength of a 5.00 g bullet that is moving at 340 m/s will it exhibite wave like properties?
View SolutionRadiation has dual nature, i.e., it possesess the properties of both, wave and particle. This prompted de-Broglie to prodict dual nature of moving material particles. Thus waves are associated with moving material particles which are called matter waves. The wavelength of matter waves is given by λ=hmv, where m is the mass, v is the speed of the particle and h is Planck's constant. Read the above paragraph and answer the following question:
(i) How was the wave nature of electron established?
(ii) What are the de-Broglie wavelength associated with a particle (i) at rest (ii) moving with infinite speed?
(iii) What are the basic values displayed by this study?
View SolutionDe-Broglie hypothesized that material particles have wave like properties. Figure shows a small particle in a box. The particle simply bounces back and forth at constant speed. As particles also have wave like properties it can be considered to be a wave reflecting back and forth from the ends of the box. The reflections will create a standing wave analogous to standing wave on a string tied at both ends. Since a standing wave confined to a region can have only selected wavelength, momentum of the particle is quantized. We can safely assume that such a particle only has kinetic energy. This energy must also be quantized.
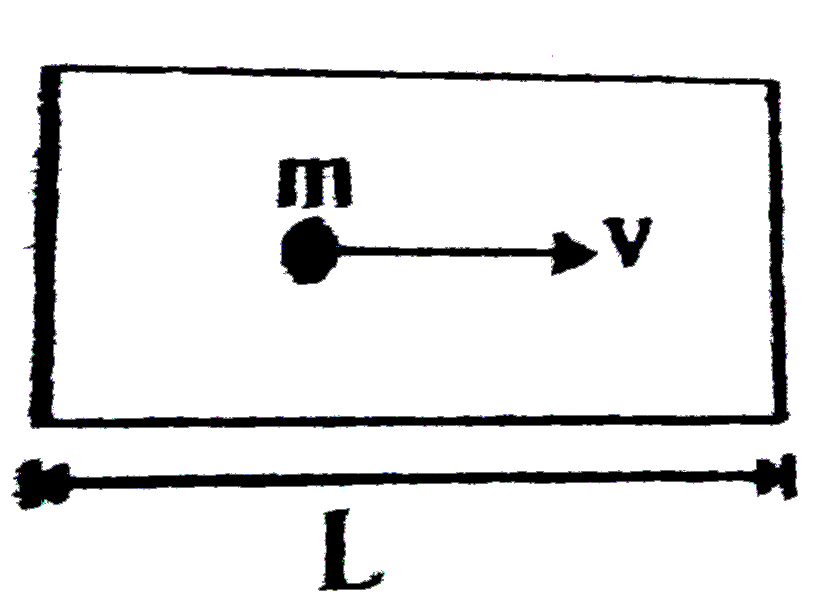
What is the particle's energy in n^(th) state?
View SolutionDe-Broglie hypothesized that material particles have wave like properties. Figure shows a small particle in a box. The particle simply bounces back and forth at constant speed. As particles also have wave like properties it can be considered to be a wave reflecting back and forth from the ends of the box. The reflections will create a standing wave analogous to standing wave on a string tied at both ends. Since a standing wave confined to a region can have only selected wavelength, momentum of the particle is quantized. We can safely assume that such a particle only has kinetic energy. This energy must also be quantized.
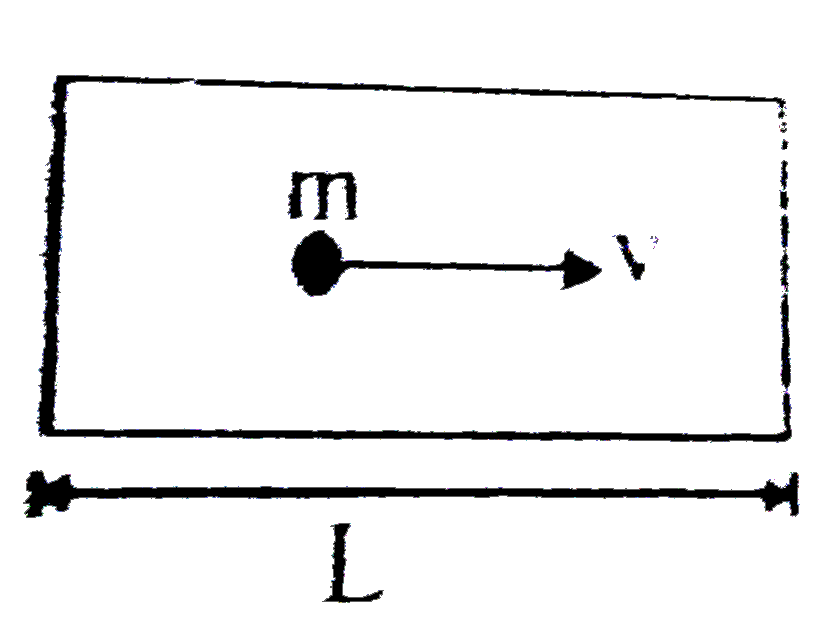
Mark the incorrect option.
View SolutionDe-Broglie hypothesized that material particles have wave like properties. Figure shows a small particle in a box. The particle simply bounces back and forth at constant speed. As particles also have wave like properties it can be considered to be a wave reflecting back and forth from the ends of the box. The reflections will create a standing wave analogous to standing wave on a string tied at both ends. Since a standing wave confined to a region can have only selected wavelength, momentum of the particle is quantized. We can safely assume that such a particle only has kinetic energy. This energy must also be quantized.
Bohr model is applied to signly ionized helium He+ Consider the lines that lie in the visible region of the spectrum. Which of the following transitions can given a photon of visible light?
View Solution
