The area bounded by the curves y= x2-2x-1, ex+y+1=0 and ordinates x=-1 and x= 1 is-
A
(3e2+2e−3)/3e
B
(e2+1)/e
C
(3e2−2e+3)/3
D
None of these
Text Solution
The correct Answer is:A
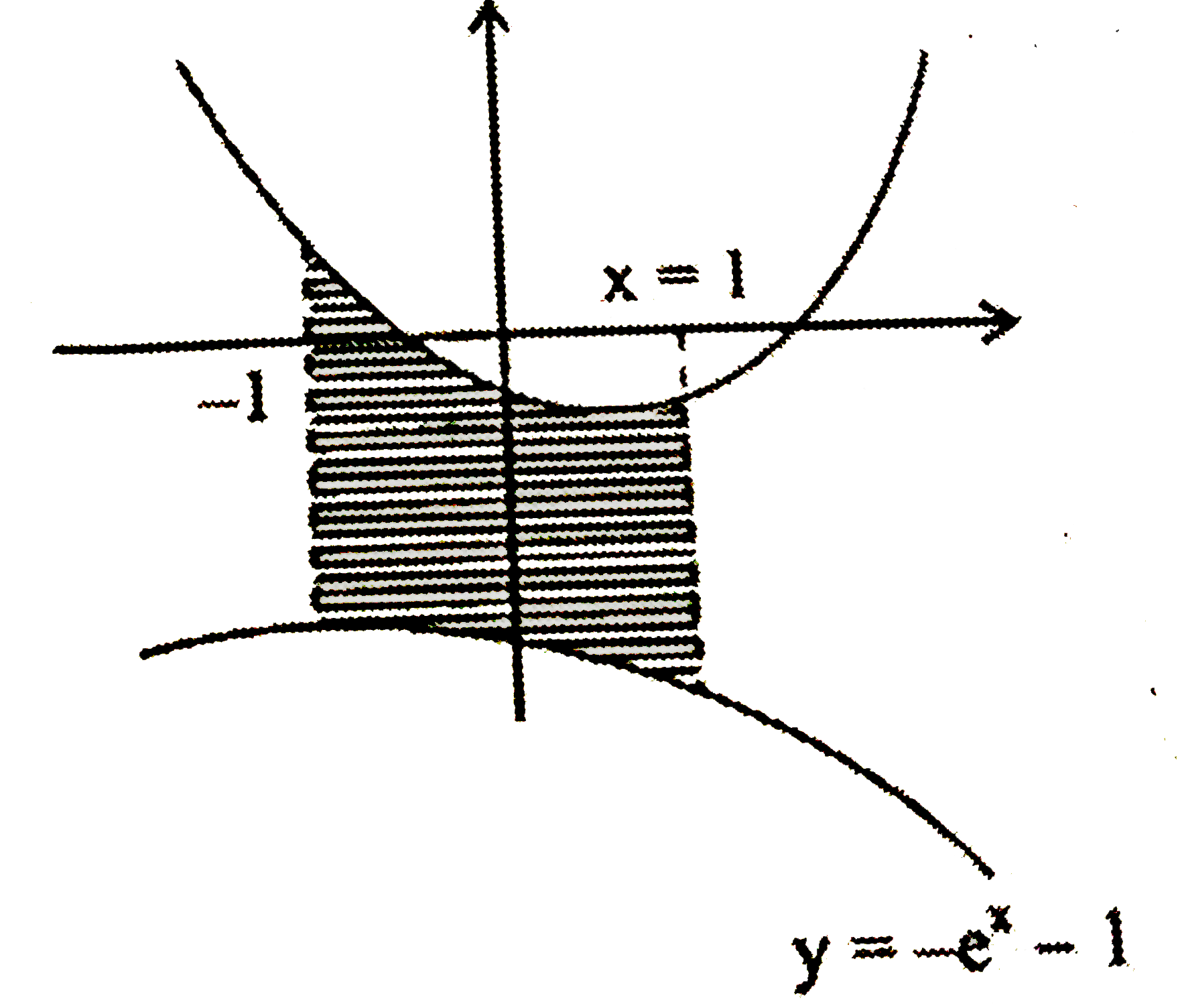
Required area
= ∫1−1(x2−2x−1)−(−ex−1)dx ltBrgt =23+e−1e
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Area bounded by the curve y=x2, the x-axis and the ordinates x=−2andx=1 is :
A−9B−154C154D174The area bounded by the curve y=x(x2−1) and x-axis is
A0B12C1D14Area bounded by the curve y=x3, the x-axis and the ordinates x=−2andx=1 is
A-9B−154C154D174
Find the area bounded by the curve y=4x−x2, the x-axis and the ordinates x=1 and x=3.
View SolutionArea bounded by the curve y=x3, the x-axis and the ordinates x=−2 and x=1 is:
View SolutionThe area bounded by the curve y=4x2 ,x-axis and the ordinates x=1,x=3 is
View SolutionFind the area bounded by the curves y2−x−1=0 and y2+x−1=0.
View SolutionThe area in square units bounded by the curves y=x3,y=x2 and the ordinates x=1,x=2 is
View Solution
