AB and CD are smooth, parallel rails, separated by a distance L and inclined to the horizontal at an angle θ. A uniform magnetic field of magnitude B, directed vertically upwards, exists in the region. EF is a conductor of mass m, carrying a current i. For EF to be in equilibrium
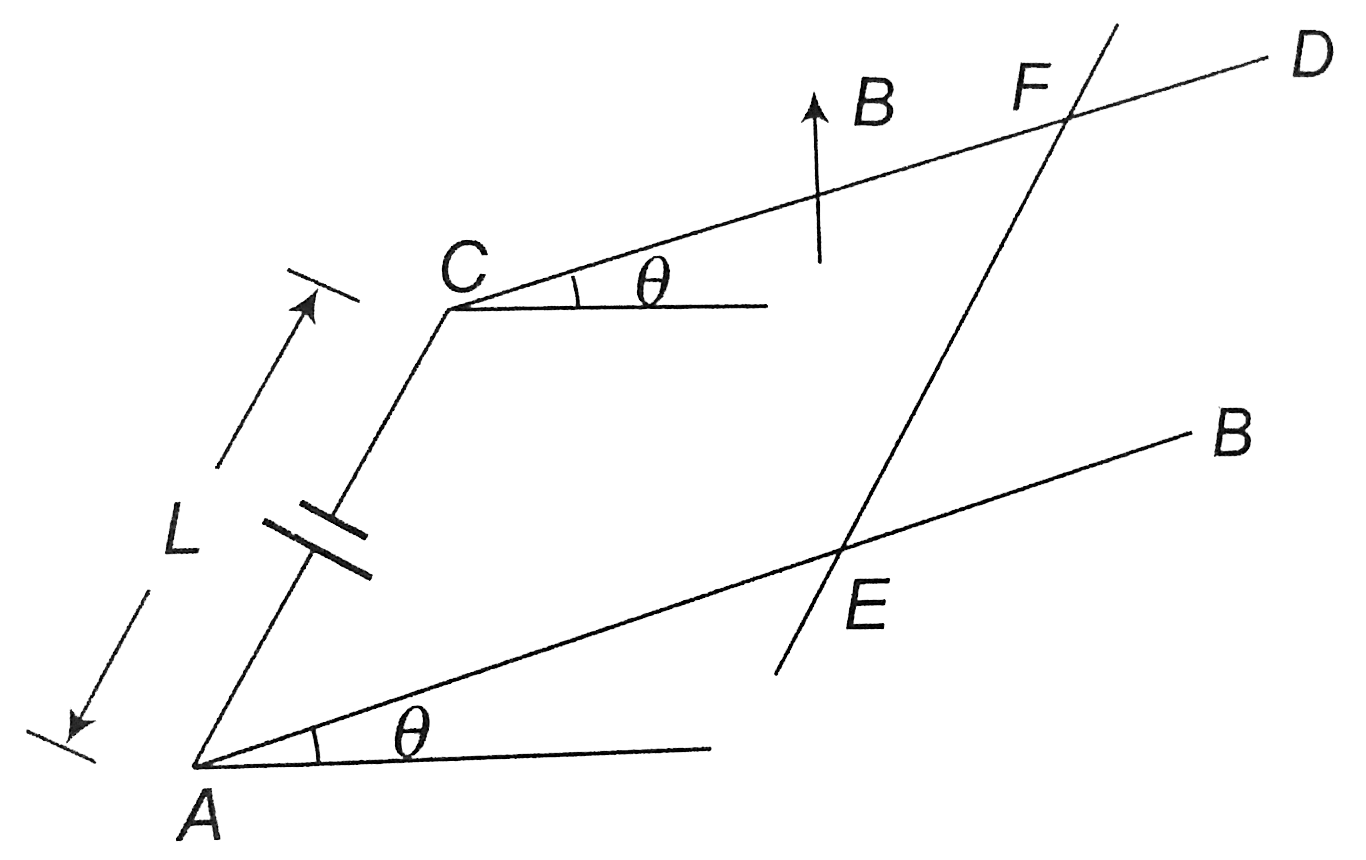
(i) i must flow from E to F
(ii) BiL=mgtanθ
(iii) BiL=mgsinθ
(iv) BiL=mg
1 must flow from E to F
BIL =mg cos θ
BIL=mg sin θ
BIL =mg
The correct Answer is:A
(1)
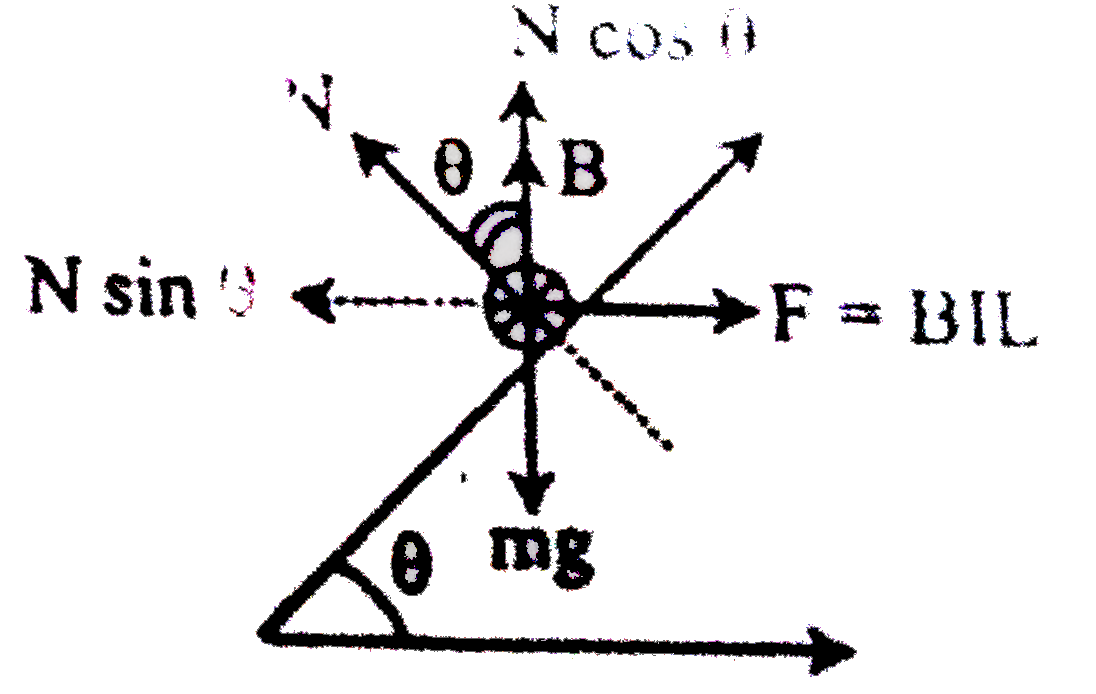 N cos θ=mg
N cos θ=mg
[⊗ indicates current 1 is flowing into the paper]
N sin θ =BIL
∴tanθ=BILmg
Topper's Solved these Questions
Similar Questions
Knowledge Check
A uniform electric field →E directed vertically upwards exists in a region of space. A point mass m carrying positive charge q is a state of equilibrium inside this electric field
AThe point mass in in stable equilibriumBThe point mass in in unstable equilibriumCThe point mass is in a state of neutral equilibriumDEquilibrium is not possibleA conductor ABCDE, shaped as shown, carries current I. It is placed in the x-y plane with the end A and E on the x-axis. A uniform magnetic field of magnitude B exists in the region. The force acting on it will be
 Azero, if B is in the x-directionBλBI in the z-direction, if B is in the y-directionCλBI in the negative y-direction,if B is in the z-directionDλaBI, if B is in the x-direction
Azero, if B is in the x-directionBλBI in the z-direction, if B is in the y-directionCλBI in the negative y-direction,if B is in the z-directionDλaBI, if B is in the x-directionThe magnetic field at centre of a hexagonal coil of side l carrying a current I is
 A√3μ0IπlBμ0I4πlCπμ0I√3lDzero
A√3μ0IπlBμ0I4πlCπμ0I√3lDzero
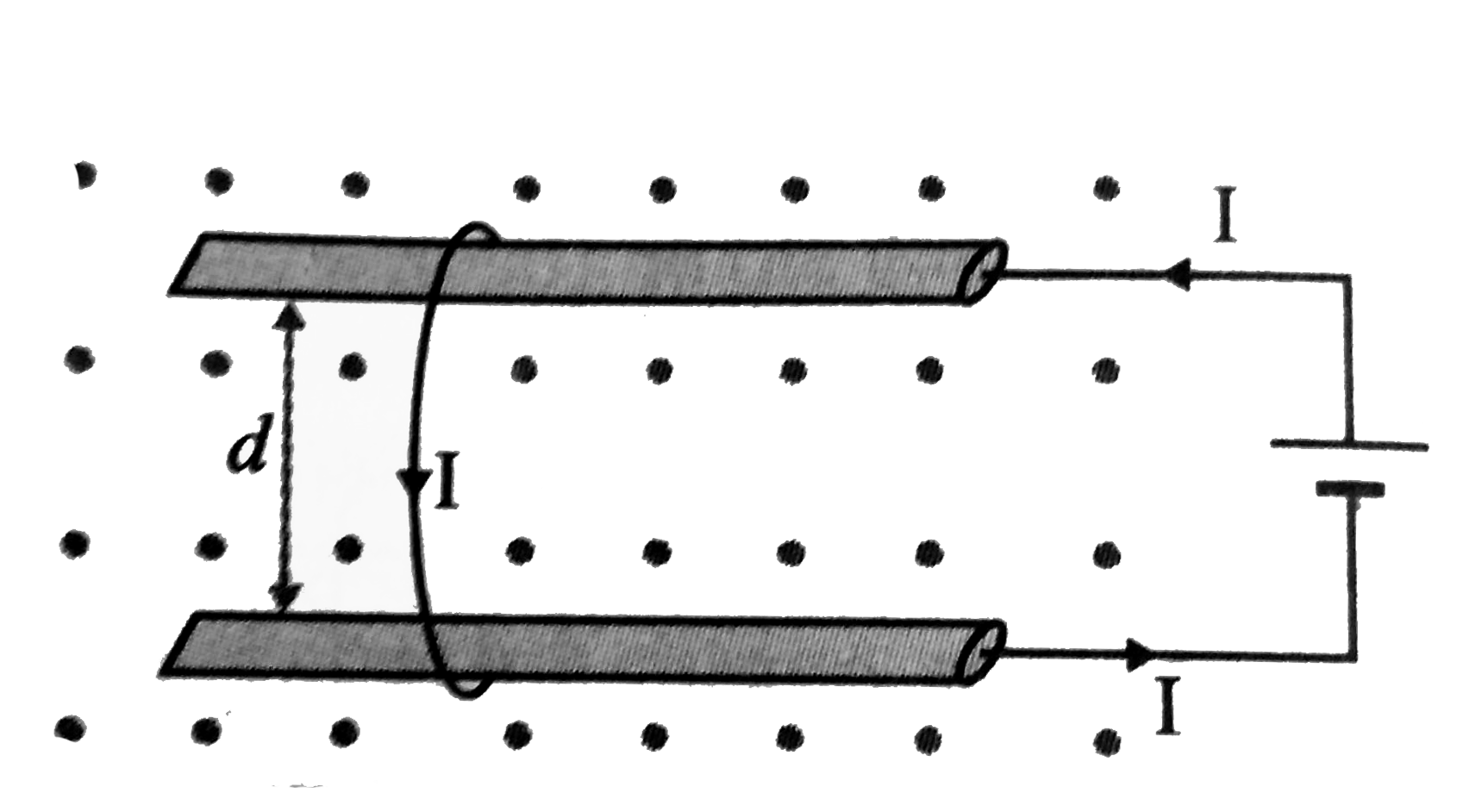
A metal wire of mass m slides without friction on two horizontal rails spaced distance d-apart as shown in figure. The rails are situated in a uniform magnetic field B, directed vertically upwards, and a battery is sending a current I through them. Find the velocity of the wire as a function of time, assuming it to be at rest initially.
View SolutionDerive an expression for the maximum force experienced by a straight conductor of length l, carrying a current I and kept in a uniform magnetic field B.
View SolutionA straight conductor of length L and carrying a current I is kept in a uniform magnetic field of induction →B. Write the expressions for the force on the conductor and the magnitude of the maximum force.
View SolutionA flat coil of n turns, area A and carrying a current I is placed in a uniform magnetic field of magnitude B. The plane of the coil makes an angle θ with the direction of the field. The torque acting on the coil is
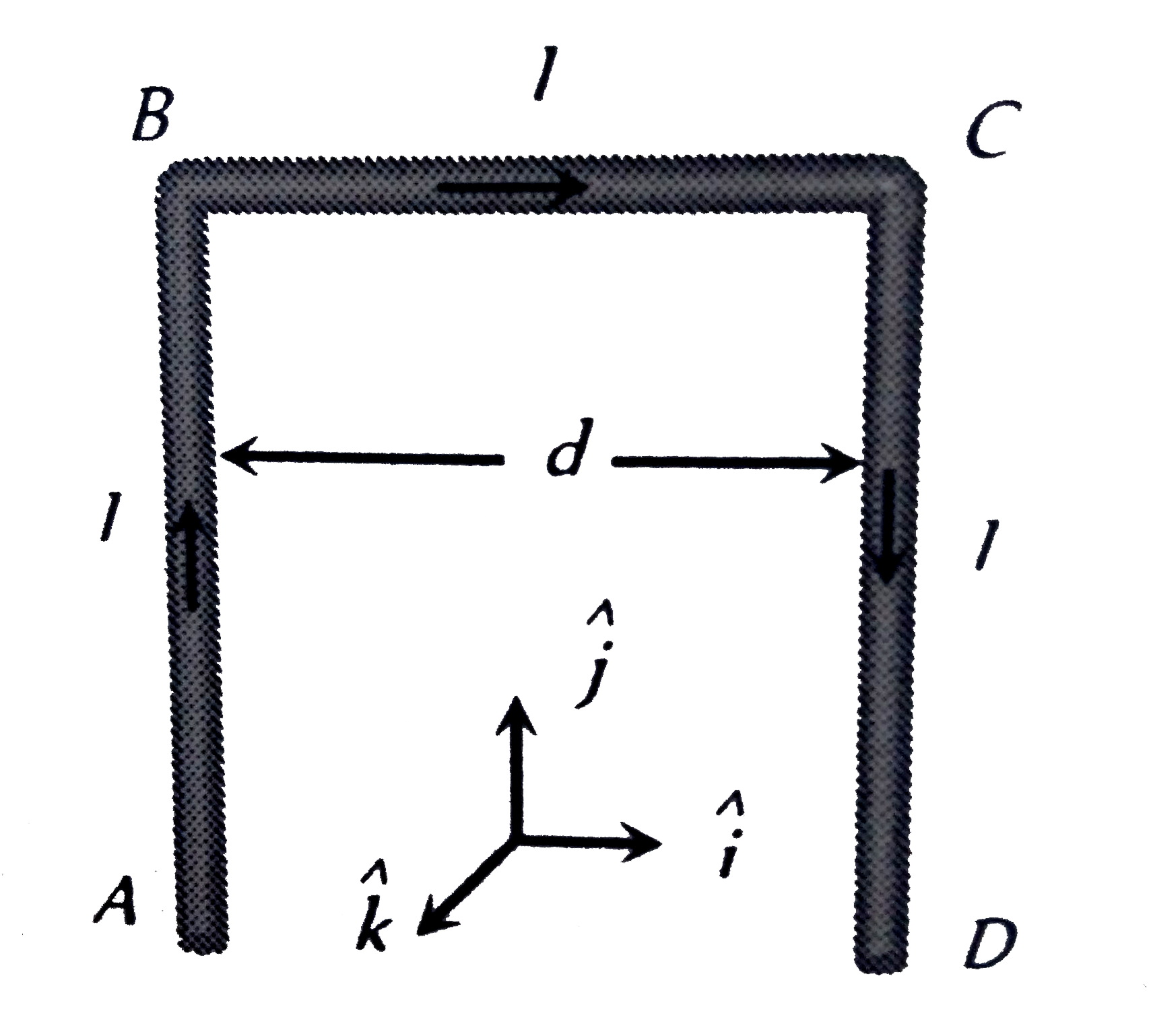
View SolutionAB and CD are long straight conductor, distance d apart, carrying a current I. The magnetic field at the midpoint of BC is
View Solution
