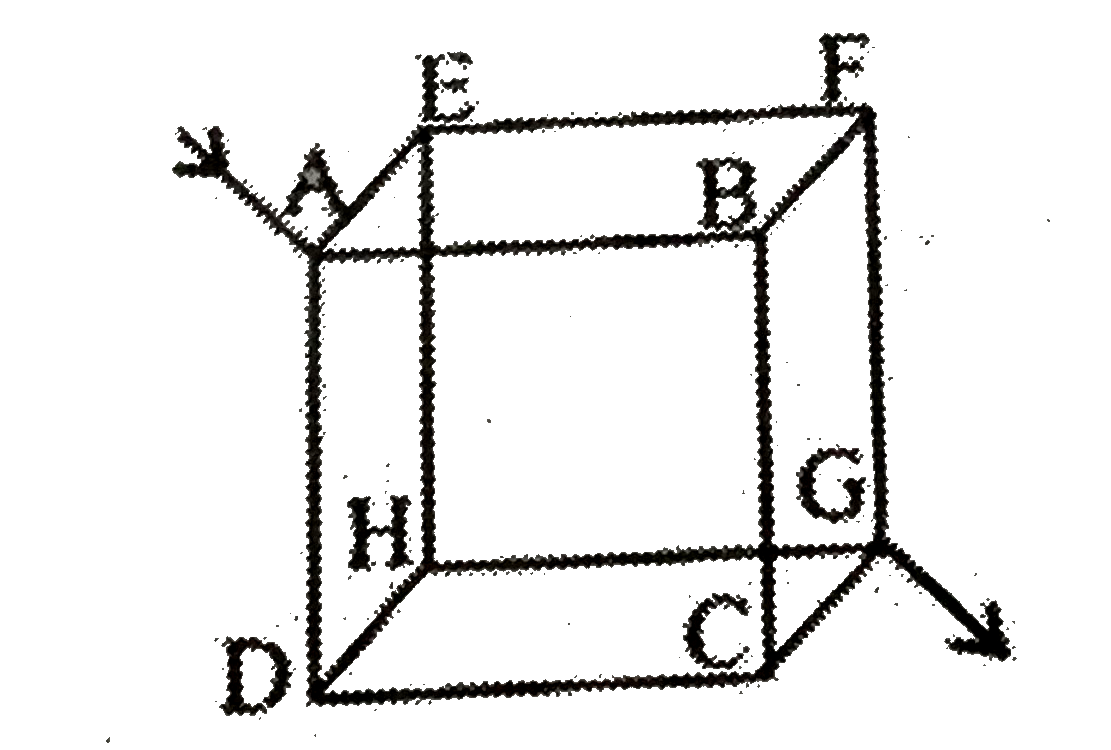
Twelve wires each of resistance 6Ω are connected to from a cube as shown in the adjoining figure. The current enters at a cornet A and leaves at erhe diagonally opposite corner G. The equivalent resistance across the corners A and G is
12Ω
6Ω
3Ω
5Ω
The correct Answer is:D

RAG=R3+R6+R3=5R6=56×6Ω=5Ω
Topper's Solved these Questions
Similar Questions
A regular hexagon is formed by six wires each of resistance rΩ and the corners are joined to the center by wires of the same resistance. If the current enters at one corner and leaves at the opposite corner, find the equivalent resistance of the conductor.
View SolutionTwelve resistors each of resistance 1Ω are connected in the circuit shown in figure. Net resistance between point A and H would be

View Solution
Knowledge Check
Twelve wires, each of resistance 1Ω are connected to form a skeleton cube. Battery of 10V and neglibible internal resistance is connected across diagonally opposite corners of the cube. Determine the equivalent resistance of the network and current supplied by the battery.
A56Ω and 12AB65Ω and 12 AC56Ω 4AD65Ω and 4ATwelve resistors each of resistance 1Ω are connected in the circuit shown in figure. Net resistance between point A and H would be
 A53ΩB163ΩC157ΩD192Ω
A53ΩB163ΩC157ΩD192ΩEight resistances each of resistance 5Ω are connected in the circuit as shown in figure. The equivalent resistance between A and B is
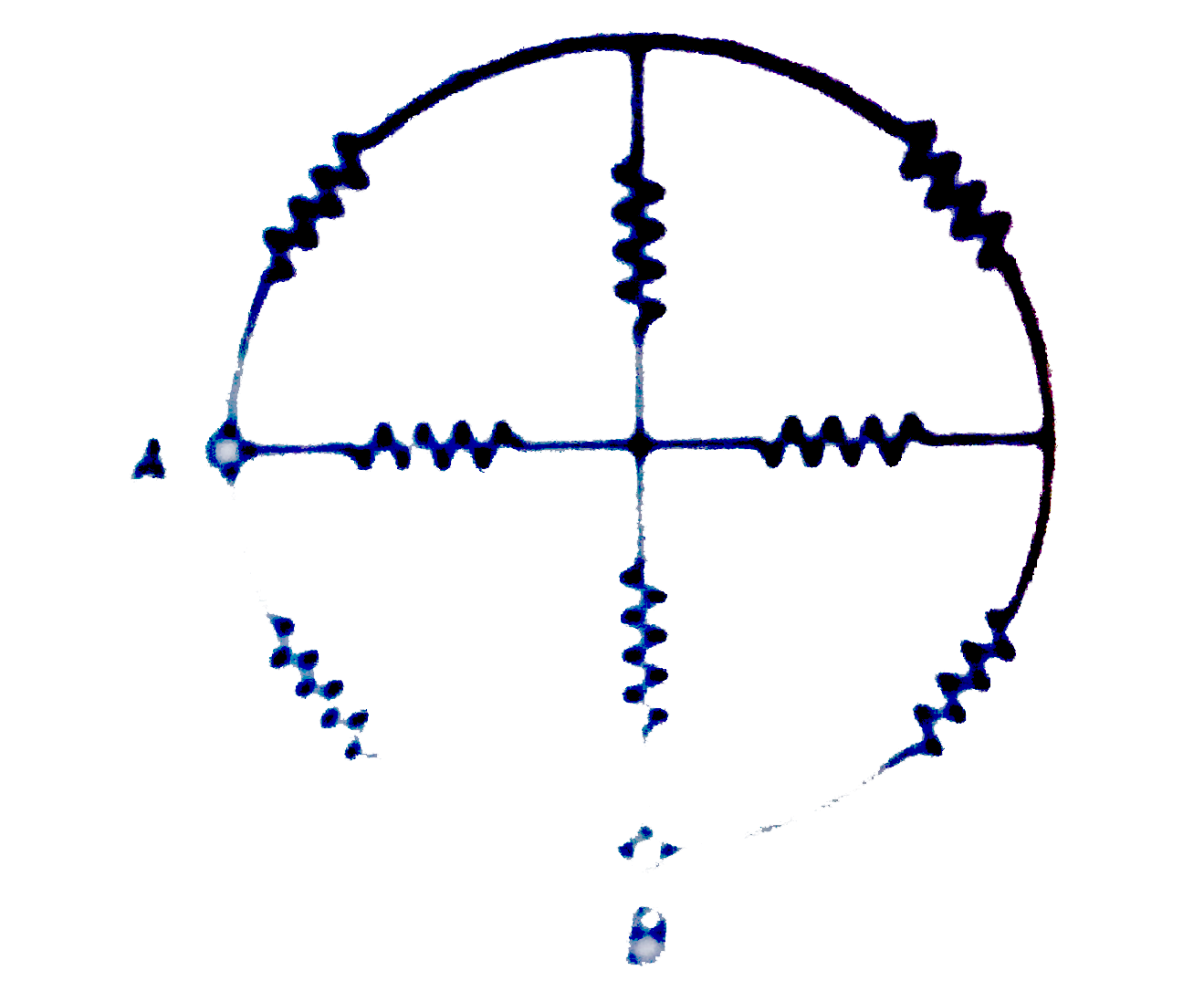 A83ΩB163ΩC157ΩD192Ω
A83ΩB163ΩC157ΩD192Ω
Nine wires each of resistance r=5Ω are connected to make a prism as shown in the figure.Find the equivalent resistance of the arrangement across AB(in Ω)
View Solution
Twelve indentical resistance each of resistance R are joined to form a cube as shown in figure. Find resistance of the combination across AB.
View SolutionEight resistances each of resistance 5Ω are connected in the circuit as shown in figure. The equivalent resistance between A and B is

View SolutionTwelve identical wires each of resistance 6Ω are arranged to from a skelence cube. A current of 40mA is led cube at the current and out at the diagonally opposite corner. Calculate the potential difference development across these current and the effective resistance of the network
View SolutionTwelve wires, each of resistance 6Ω are connected to form a cube. The effective resistance between two diagonally opposite corners of the cube is
View Solution
