Find the sines and cosines of all angles in the first four quadrants whose tangents are equal to cos135∘
cos135=−1√2
tanp=−1√2
sinp=1√2(in second quater)
=−1√2( in fourth quater)
cos(P)=−1√2(in second quadrent)
=1√2( in fourth quadrent).
Similar Questions
Find the sines and cosines of all angles in the first four quadrants whose tangents are equal to cos135∘
View SolutionFind the sine and cosine of angle θ shown in the unit circle if coordinate of point p are as shown.
View SolutionFind the sine and cosine of angle θ shown in the unit circle if coordinate of point p are as shown.
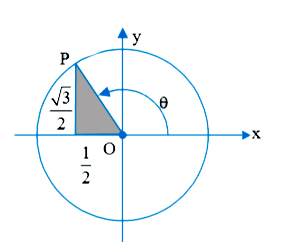
View SolutionFind the sine and cosine of angle θ shown in the unit circle if coordinate of point p are as shown.

View SolutionFind the direction cosines of a line which makes equal angles with the coordinate axes.
View SolutionFind the direction cosines of a line which makes equal angles with the coordinate axes.
View SolutionFind the direction cosines of a vector which makes equal angles with the axes.
View SolutionFind the angle θ whose cosine is equal to its tangent.
View SolutionFind the angle θ whose cosine is equal to its tangent.
View SolutionThe product of the sines of the angles of a triangle is p and the product of their cosines is q. Show that the tangents of the angles are the roots of the equation qx3−px2+(1+q)x−p=0.
View Solution
