For the values x1,x2........x100 of a distribution x1<x2<x3<......<x100<x101. The mean deviation of this distribution with respect to anumber k will be minimum when k is equal to
Step by step video & image solution for For the values x_1,x_2........x_100 of a distribution x_1 lt x_2 lt x_3 lt......lt x_100 lt x_101. The mean deviation of this distribution with respect to anumber k will be minimum when k is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Consider any set of observations x1,x2,x3,..,x101. It is given that x1<x2<x3<..Ltx100<x101, then the mean deviation of this set of observations about a point k is minimum when k equals
View SolutionA random variable X has the following distribution .

The value of k and P(X<4) are equal to
View Solution
Knowledge Check
Consider any set of observations x1,x2,x3,..,x101. It is given that x1<x2<x3<..Ltx100<x101, then the mean deviation of this set of observations about a point k is minimum when k equals
Ax1Bx51Cx1+x2+..+x101101Dx50Consider any set of 201 observations x1,x2,…,x200,x201. It is given that x1<x2<…<x200<x201. Then, the mean deviation of this set of observations about a point k is minimum, when k equals
A(x1+x2+…+x200+x201)201Bx1Cx101Dx201If x1andx2 are the means of two distributions such that x1<x2and¯x is the mean of the combined distribution, then
A¯x<¯x1B¯x>¯x2C¯x=¯x1+¯x22D¯x1<¯x<¯x2
The probability distribution of X is as follows:
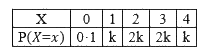
Find k and P [X<2].
View SolutionIf the median of the scores 1,2,x,4,5(where 1<2<x<4<5) is 3, then the mean of the scores is
View SolutionIf 2x+4(x−3)<−2−x<2x−1, then find the value of x. (a) -1 (b) 1 (c) 2 (d) -2
View SolutionIfoverline(x_1)andoverline(x_2)aremeansoftwodistributionssuchtˆoverline(x-1) lt overline(x_2)andoverlinex is distribution, then
View SolutionIf 4(x+1)−3<3−x<2x+5, then the value of x is
View Solution
