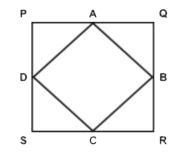
ABCDandPQRS are two variable rectangles, such that A,B,CandD lie on PQ,QR,RS and SP respectivelyand perimeter , 'x' of ABCD is constant. If the maximum area of PQRS is 32, then x4
Step by step video & image solution for ABCD and PQRS are two variable rectangles, such that A,B,C and D lie on PQ,QR,RS and SP respectivelyand perimeter , 'x' of ABCD is constant. If the maximum area of PQRS is 32, then x/4 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
19. ABCD is a rectangle having length (x 1) and breadth (x- 1). If P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively, then the perimeter of quadrilateral PQRS is
View SolutionIf points A and B lie on x-axis and points C and D lie on the curve y=x2−1 below the x-axis then maximum area of rectangle ABCD is
View Solution
Knowledge Check
PQRS is a square with side 10 cm. A, B, C and D are mid-points of PQ, QR, RS and SP respectively. Then the perimeter of the square ABCD so formed is
A10√2cmB20√2cmC25√2cmD15√2cmPQRS is a rectangle, A, B, C and D are the mid points of sides PQ, QR, RS and PS respectively. If area of ΔPQR is 48 cm2, then what is the area (in cm2) of ΔBCD?
A24B6C16D12PQRSis a rectangle. Points A, B, C and D are the mid points of sides PQ,QR,RSandPSrespectively. If area of ΔPQR is 48cm2, then what is the area (in cm) of ΔBCD?
A24B6C16D12
One of the diameter of a circle circumscribing the rectangle ABCD is 4y=x+7, If A and B are the points (−3,4) and (5,4) respectively, then the area of rectangle is
View SolutionPQRS is a quadrilateral having 3 4 5 6 points on PQ , QR, RS and SP respectively. The number of triangles with vertices on different sides is
View SolutionPoints A, B, C and D are midpoints of the sides of square PQRS. If the area of PQRS is 36 Sqcm, the area of ABCD is ...........Sqcm
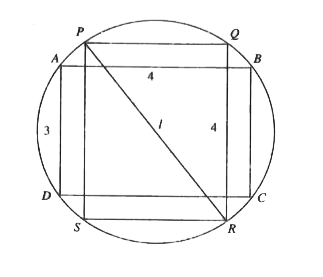
View SolutionIn the figure, ABCD and PQRS are two rectangle inscribed in the circle as shown and AB = 4, AD = 3 and QR = 4. what is the value of l ?
View SolutionIf points A and B lie on x-axis and points C and D lie on the curve y=x2−1 below the x-axis then maximum area of rectangle ABCD is
View Solution
