Earth's orbit is an ellipse with eccentricity 0.0167. Thus, the earth's distance from the sun and speed as it moves around the sun varies from day-to-day. This means that the length of the solar day is not constant through the year. Assume that the earth's spin axis is normal to its day. A day should be taken from noon to noon. Does this explain variation of length of the during the year ?

Text Solution

Verified by Experts

Consider the diagram. Let $m$ be the mass of the earth, $v_{p}, v (a)$ be the velocity of the earth at perigee and apogee respectively. Similarly, $ω_{p}$ and $ω_{a}$ are corresponding angular velocities.

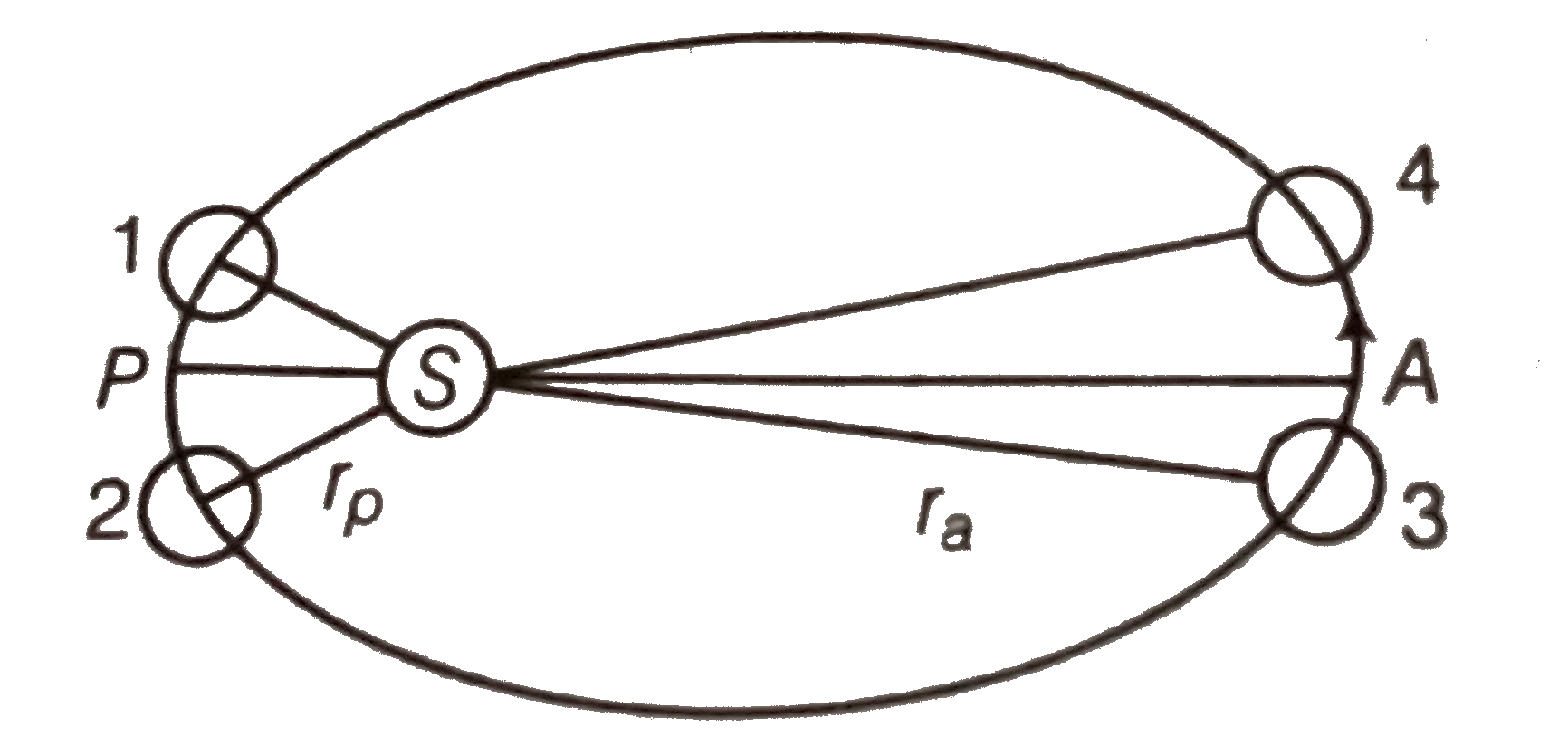
Angular momentum and areal velocity are constant as the earth orbits the sun
At perigee, $r_{p}^{2} ω_{p} = r_{a}^{2} ω_{a}$ at apogee ....(i)
If a is the semi-major axis of the earth's orbit, then $r_{p} = a (1 - e) and r_{a} = a (1 + e)$ ....(ii)
$∴ \frac{ω_{p}}{ω_{a}} = {(\frac{1 + e}{1 - e})}^{2}, e = 0.0167$ [from Eqs. (i) and (ii)]
$∴ \frac{ω_{p}}{ω_{a}} = 1.0691$
Let $ω$ be angular speed which is geometric mean of $ω_{p}$ and $ω_{a}$ and corresponds to mean solar day,
$∴ (\frac{ω_{p}}{ω}) (\frac{ω}{ω_{a}}) = 10691$
$∴ \frac{ω_{p}}{ω} = \frac{ω}{ω_{a}} = 1034$
If $ω$ corresponds to $1^{\circ}$ per day (mean angular speed), then $ω_{p} = 1034^{\circ}$ per day and $ω_{a} = {0.967}^{\circ}$ per day. Since, $361^{\circ} = 24$ , mean solar day, we get 361.034 which corresponds to $24 h, 8.14''$ (8.1'' longer) and ${360.967}^{\circ}$ corresponds to $23 h 59 min 52''$ (7.9'' smaller).
This does not explain the actual variation of the length of the day during the year.

Updated on:21/07/2023