If the median AD of triangle ABC divides the angle BAC in the ratio 1:2, then show that sinBsinC=12sec(A3).
Video Solution
|
Answer
Step by step video & image solution for If the median AD of triangle ABC divides the angle BAC in the ratio 1:2, then show that (sinB)/(sinC)=1/2sec(A/3). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
If the angles of a triangle ABC are in the ratio 2:3:1 then the angles A,B and C are
A∠A=60∘,an≥lB=90∘∘,∠C=30∘B∠A=40∘,an≥lB=120∘∘,∠C=20∘C∠A=20∘,an≥lB=60∘∘,∠C=60∘D∠A=45∘,an≥lB=90∘∘,∠C=45∘If the angles of a triangle ABC are in the ratio 1:2:3. then the corresponding sides are in the ratio ?
A1:2:3B3:2:1C1:√3:2D1:√3:√2If in triangle ABC, cosA=sinB2sinC, then the triangle is
AEquilateralBIsoscelesCRight angledDObtuse triangle
In a triangle ABC, if the angles are in the ratio 1:2:4, then ∑sec2A∑cosec2A=..........
View SolutionIn a ΔABC (right angled at B) , median BD of length l divides angle B in the ratio of 2:1 . Find area of ΔABC .
View SolutionIf in a triangle ABC,cosA=sinB2sinC then the triangle ABC , is
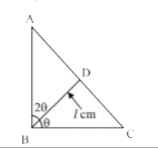
View SolutionLength of a median of a right ΔABC is l cm. That divides right angle in the ratio 1 : 2. What is the area of triangle?
View SolutionIn any triangle ABC, if cosA=sinB2sinC, then :
View Solution