A sector has an area of 40π and a radius of 10. What is the arc length of the sector?
The correct Answer is:8π
To find the arc length of a sector given its area and radius, we can follow these steps:
Step 1: Write down the formula for the area of a sector.
The area A of a sector is given by the formula:
A=θ360×πr2
where θ is the central angle in degrees and r is the radius.
Step 2: Substitute the given values into the area formula.
We know that the area A=40π and the radius r=10. Substituting these values into the formula gives:
40π=θ360×π×102
This simplifies to:
40π=θ360×π×100
Step 3: Simplify the equation.
We can cancel π from both sides:
40=θ360×100
Now, multiply both sides by 360:
40×360=θ×100
This simplifies to:
14400=θ×100
Step 4: Solve for θ.
Dividing both sides by 100 gives:
θ=14400100=144 degrees
Step 5: Convert θ from degrees to radians.
To convert degrees to radians, use the conversion factor π180:
θ (in radians)=144×π180
Simplifying this:
θ=144π180=4π5 radians
Step 6: Use the arc length formula.
The arc length L of a sector is given by:
L=r×θ
Substituting r=10 and θ=4π5:
L=10×4π5
Step 7: Simplify to find L.
Calculating this gives:
L=40π5=8π
Final Answer:
The arc length of the sector is 8π.
---
The area A of a sector is given by the formula:
A=θ360×πr2
where θ is the central angle in degrees and r is the radius.
We know that the area A=40π and the radius r=10. Substituting these values into the formula gives:
40π=θ360×π×102
This simplifies to:
40π=θ360×π×100
We can cancel π from both sides:
40=θ360×100
Now, multiply both sides by 360:
40×360=θ×100
This simplifies to:
14400=θ×100
Dividing both sides by 100 gives:
θ=14400100=144 degrees
To convert degrees to radians, use the conversion factor π180:
θ (in radians)=144×π180
Simplifying this:
θ=144π180=4π5 radians
The arc length L of a sector is given by:
L=r×θ
Substituting r=10 and θ=4π5:
L=10×4π5
Calculating this gives:
L=40π5=8π
The arc length of the sector is 8π.
Similar Questions
Knowledge Check
- Question 1 - Select One
A circle with a diameter of 8 inches is divided into a number of equal sectors such that each sector has an area of 4π3 square inches. What is the central angle of each sector, in radians
Aπ12Bπ6Cπ3D2π3 - Question 2 - Select One
Circle O (not shown) is divided into three sectores. Point P, Q and R are on the circumference of the circle. Sector POR has an area of 8π, and sector ROQ has an area of 6π. IF the radius of circle O is 4, what is the measure of the central angle of sector QOP, in degrees?
A45B90C135D180 - Question 3 - Select One
If a sector of a circle has an arc length of 2π inches and an area of 6π square inches, what is the length of the radius of the circle?
A1B2C3D6
What is the area of the sector shown in
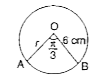 View Solution
View SolutionIf the adjoining figure is a sector of a circle of radius 10.5 cm, what is the perimeter of the sector? (Take π=22/7 ) (FIGURE)
View SolutionThe perimeter of a certain sector of a circle of radius 5.7 m is 27.2 m. find the area of the sector
View SolutionThe perimeter of a certain sector of a circle of radius 5.6 m is 27.2 m. Find the area of the sector
View SolutionThe perimeter of a certain sector of a circle of radius 5.7 m is 27.2 m. Find the area of the sector.
View Solution

