A unit square is circumscribed about a circle. If the circumference of the circle is qπ, what is the value of q?
1
2
π
2π
To solve the problem, we need to determine the value of q given that a unit square is circumscribed about a circle, and the circumference of the circle is expressed as qπ.
1. Understand the Unit Square and Circle:
- A unit square has sides of length 1. When a circle is circumscribed about this square, the circle touches the midpoint of each side of the square.
2. Determine the Diameter of the Circle:
- The diameter of the circle is equal to the side length of the square, which is 1. Therefore, we have:
D=1
3. Calculate the Radius of the Circle:
- The radius r of the circle is half of the diameter:
r=D2=12
4. Use the Formula for Circumference:
- The formula for the circumference C of a circle is given by:
C=2πr
- Substituting the radius we found:
C=2π(12)=π
5. Set the Circumference Equal to qπ:
- According to the problem, the circumference is also expressed as qπ:
C=qπ
- Since we calculated C=π, we can set the two expressions equal to each other:
π=qπ
6. Solve for q:
- To find q, we can divide both sides of the equation by π (assuming π≠0):
1=q
- Thus, we find:
q=1
Final Answer:
The value of q is 1.
- A unit square has sides of length 1. When a circle is circumscribed about this square, the circle touches the midpoint of each side of the square.
- The diameter of the circle is equal to the side length of the square, which is 1. Therefore, we have:
D=1
- The radius r of the circle is half of the diameter:
r=D2=12
- The formula for the circumference C of a circle is given by:
C=2πr
- Substituting the radius we found:
C=2π(12)=π
- According to the problem, the circumference is also expressed as qπ:
C=qπ
- Since we calculated C=π, we can set the two expressions equal to each other:
π=qπ
- To find q, we can divide both sides of the equation by π (assuming π≠0):
1=q
- Thus, we find:
q=1
The value of q is 1.
Similar Questions
Knowledge Check
If p is the circumference of the circle Q and the area of the circle is 25π, what is the value of p?
A25B10πC35D15πIf the area of a circle is 64π, which is the circumference of the circle?
A8πB16πC32πD64π
If the circumference of the circle above is 16π, what is the total area of the shaded regions?A64πB32πC12πD8π
The area of a circle is 25π. What is the circumference?
View Solution
In the circle above, point A is the center and the length of arc ⌢BC is 25 of the circumference of the circle. What is the value of x ?
View SolutionIn figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle . Is the area of the outer square four times the area of the inner square ? Give reason for your answer.

View Solution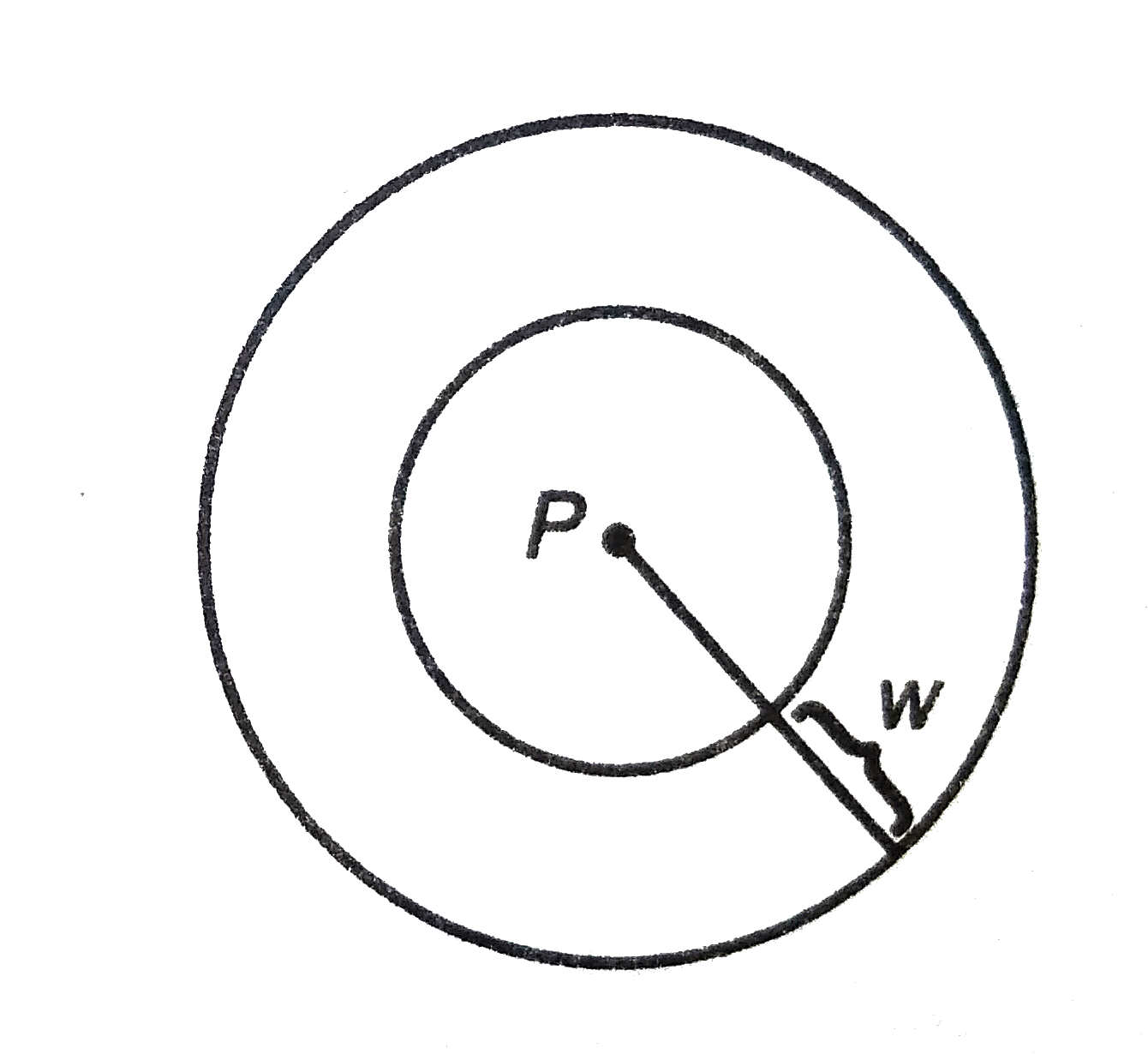
In the figure above, point P is the center of each circle. The circumference of the larger circle exceeds the circumference of the smaller circle by 12π. What is the width, w, of the region between the two circles?
View SolutionWhat is the radius of a circle whose circumference is π?
View Solution
