A capacitor ' "c'" is charged to a potential "difference "V" and then it is connected to an uncharged capacitor of capacitance "'3c'." Now total loss is "(3(β−1)cv2)" .The value of "β" is "]
Step by step video & image solution for A capacitor ' "c'" is charged to a potential "difference "V" and then it is connected to an uncharged capacitor of capacitance "'3c'." Now total loss is "((3)/((beta-1))cv^(2))" .The value of "beta" is "] by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A capacitor of capacity C charged to potential "V" and " then connected to an identical uncharged capacitor then loss of energy is
View SolutionA capacitor of capacitance 2.0μF is charged to a potential difference of 12 V. It is then connected to an uncharged capacitor of capacitance 4.0μF. Find (a) the charge flow through connecting wire upto study strate on each of the two capacitors after the connection in μC (b) The total electrostatic energy stored in both capacitors in μJ (c) the heat produced during the charge transfer from one capacitor to the other in μJ.
View Solution
Knowledge Check
- Question 1 - Select One
A capacitor C is charged to a potential difference V and battery is disconnected. Now if the capacitor plates are brough close slowely by some distance:
Asome +ve work is done by external agentBenegry of capacitor will decreaseCenegry of capacitor will increaseDnone of the above - Question 2 - Select One
A capacitor of capacitance C0 is charged to potential V0. Now it is connected to another uncharged capacitor of capacitance C02. Calculate the heat loss in this process.
A12C0V20B13C0V20C16C0V20D18C0V20 - Question 3 - Select One or More
A capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
AThe initial current through the resistance is VRBThe current through the resistance as a function of time is i(t)=VRe−tτ where τ=R(C1C2C1+C2)CThe charge on capacitor C1 as a function of time is q1(t)=(C1VC1+C2)(C1+C2e−tτ)DAfter a long time, the potential difference across the capacitor C1is(C1C1+C2)V
A 10μF capacitor is charged to a potential difference of 50V and is connected to another uncharged capacitor in parallel. Now the common potential difference becomes 20 volt. The capacitance of second capacitor is
View SolutionA 10μF capacitor is charged to a potential difference of 50V and is connected to another uncharged capacitor in parallel. Now the common potential difference becomes 20 volt. The capacitance of second capacitor is
View SolutionA capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
View SolutionA capacitor C1 of capacitance C is charged to a potential difference V0. The terminal of the charged capacitor are then connected to an uncharged capacitor C2of capacitance C/2. Match the entries of Column I with the entries of Column II and choose the correct option from the codes given below.
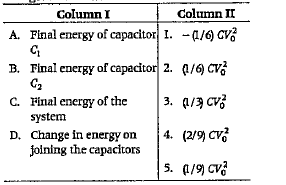 View Solution
View SolutionA capacity of capacity C1 is charged up to V volt and then connected to an uncharged capacitor of capacity C2. Then final potential difference across each will be
View Solution
