A copper conductor is in the shape of a cylindrical shell of length 20 cm and inner and outer diameter 1 cm and 3 cm. A potential difference 200 V is applied between the flat surfaces of the conductor. The current density in it is . The value of x is ________
To solve the problem step by step, we will follow these calculations:
Step 1: Identify the given values
- Length of the cylindrical shell, L=20cm=0.2m
- Inner diameter, di=1cm=0.01m (inner radius ri=0.005m)
- Outer diameter, do=3cm=0.03m (outer radius ro=0.015m)
- Potential difference, V=200V
- Resistivity of copper, ρ=10−8Ω⋅m
- Current density, J=10xA/m2
Step 2: Calculate the cross-sectional area A
The cross-sectional area A of the cylindrical shell can be calculated using the formula for the area of a ring:
A=π(r2o−r2i)
Substituting the values:
A=π((0.015)2−(0.005)2)=π(0.000225−0.000025)=π×0.0002m2
A≈0.000628m2
Step 3: Calculate the resistance R
The resistance R of the cylindrical shell can be calculated using the formula:
R=ρLA
Substituting the values:
R=10−8×0.20.000628≈2×10−90.000628≈3.18×10−6Ω
Step 4: Calculate the current I
Using Ohm's law, V=IR, we can find the current I:
I=VR=2003.18×10−6≈62.86×106A
Step 5: Calculate the current density J
Now, we can find the current density J:
J=IA=62.86×1060.000628≈1.000×1011A/m2
Step 6: Determine the value of x
Since we have J=10xA/m2, we can equate:
10x=1.000×1011
Thus, x=11.
Final Answer
The value of x is 11.
---
- Length of the cylindrical shell, L=20cm=0.2m
- Inner diameter, di=1cm=0.01m (inner radius ri=0.005m)
- Outer diameter, do=3cm=0.03m (outer radius ro=0.015m)
- Potential difference, V=200V
- Resistivity of copper, ρ=10−8Ω⋅m
- Current density, J=10xA/m2
The cross-sectional area A of the cylindrical shell can be calculated using the formula for the area of a ring:
A=π(r2o−r2i)
Substituting the values:
A=π((0.015)2−(0.005)2)=π(0.000225−0.000025)=π×0.0002m2
A≈0.000628m2
The resistance R of the cylindrical shell can be calculated using the formula:
R=ρLA
Substituting the values:
R=10−8×0.20.000628≈2×10−90.000628≈3.18×10−6Ω
Using Ohm's law, V=IR, we can find the current I:
I=VR=2003.18×10−6≈62.86×106A
Now, we can find the current density J:
J=IA=62.86×1060.000628≈1.000×1011A/m2
Since we have J=10xA/m2, we can equate:
10x=1.000×1011
Thus, x=11.
The value of x is 11.
Similar Questions
A conductor in the shape of a cylindrical shell of outer and inner radii 2r and r is connected to an ideal battery as shown. The length of the conductor is m. The charge carrier density in the conductor is n×8×10283−3 The value of r=16cm If the current through the battery is 4A, the drift velocity of electrons at a distance 1.5r from the axis of the conductor is ___________ ×10−6m/s .
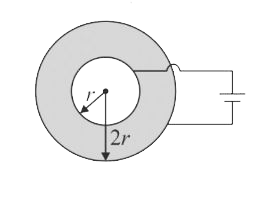 View Solution
View SolutionA potential difference 100 V is applied across a conductor which is a cylindrical shell of inner and outer diameter 2 cm and 4 cm respectively and length 10 cm. Current flows in a direction parallel to the axis of the conductor. If heat is dissipated in the conductor at the rate 15 W, the resistivity of the material of the conductor is _________ Ωm. [Take π=228]
View Solution
Knowledge Check
- Question 1 - Select One
Two plates are 2cm apart, a potential difference of 10 volt is applied between them, the electric field between the plates is
A20N/CB500N/CC5N/CD250N/C - Question 2 - Select One
A potential difference of 5V is applied across a conductor of length 10 cm. IF drift of electron is 2.5×104m/s, then electron mobility is SI unit is
A5×10−4B5×10−6C5×10−2DZero - Question 3 - Select One
A potential difference of 5 V is applied across a conductor of length 10 cm . If drift velcoity of electrons is 2.5×10−4m/s , then electron mobility will be
A5×10−4m2V−1S−1B5×10−6m2V−1s−1C5×10−2m2V−1s−1DZero
Find the resistance of a hollow cylindrical conductor of length 1.0m and inner and outer radii 1.0mm and 2.0mm respectively. The resistivity of the material is 2.0×10−8(Ω)m.
View SolutionConsider a conductor of length 40 cm where a potential difference of 10V is maintained between the ends of the conductor. Find the mobility of the electrons provided the drift velocity of the electrons is 5×10−6ms−1
View SolutionFind the resistance of a hollow cylindrical conductor of length 1.0m and inner and outer radii 1.0mm and 2.0mm respectively. The resistivity of the material is 2.0×10−8(Ω)m.
View SolutionThe inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1 cm3 of wood has a mass of 0.6 g.
View SolutionThe space between two concentric conducting spherical shells of radii b=1.70 cm and a=1.20 cm is filled with a substance of dielectric constant k=6.91 A. A potential difference V=73.0 V is applied across the inner and outer shells Determine (a) the capacitance of the device (b) the free charge q on the inner shell, and (c) the charge q induced along the surface of the inner shell?
View Solution

