A fuse wire melts when a currentIm is passed through it. The value of Im can be increased by:
[Assume that each change is made while keeping the other quantities fixed]
Decreasing the resistivity of the wire
Decreasing the area of cross-section of the wire
Increasing the resistivity of the wire
Increasing the melting point of the wire
To determine how the value of Im (the maximum current that a fuse wire can carry before melting) can be increased, we need to analyze the relationship between current, voltage, and resistance in the context of Ohm's Law.
1. Understand the relationship between current, voltage, and resistance:
According to Ohm's Law, the current I flowing through a conductor is given by the formula:
\(
I = \frac{V}{R}
\)
where V is the voltage across the conductor and R is the resistance of the conductor.
2. Identify the parameters affecting resistance:
The resistance R of a fuse wire can be expressed as:
\(
R = \rho \frac{L}{A}
\)
where:
- ρ is the resistivity of the material,
- L is the length of the wire,
- A is the cross-sectional area of the wire.
3. Analyze how to increase Im:
Since the voltage V is constant (as stated in the problem), to increase the maximum current Im, we need to decrease the resistance R. This can be achieved by:
- Decreasing the resistivity ρ of the wire material.
- Decreasing the length L of the wire.
- Increasing the cross-sectional area A of the wire.
4. Evaluate the options:
- Decreasing the resistivity of the wire: This will decrease R, thus increasing Im.
- Decreasing the length of the wire: This will also decrease R, thus increasing Im.
- Increasing the cross-sectional area of the wire: This will decrease R, thus increasing Im.
- Increasing the melting point of the wire: This does not affect the resistance directly and is irrelevant to increasing Im.
5. Conclusion:
The only viable options to increase Im are to decrease the resistivity of the wire, decrease the length of the wire, or increase the cross-sectional area of the wire. Among these, the most straightforward method is to decrease the resistivity of the wire.
Final Answer:
The value of Im can be increased by decreasing the resistivity of the wire.
---
According to Ohm's Law, the current I flowing through a conductor is given by the formula:
\(
I = \frac{V}{R}
\)
where V is the voltage across the conductor and R is the resistance of the conductor.
The resistance R of a fuse wire can be expressed as:
\(
R = \rho \frac{L}{A}
\)
where:
- ρ is the resistivity of the material,
- L is the length of the wire,
- A is the cross-sectional area of the wire.
Since the voltage V is constant (as stated in the problem), to increase the maximum current Im, we need to decrease the resistance R. This can be achieved by:
- Decreasing the resistivity ρ of the wire material.
- Decreasing the length L of the wire.
- Increasing the cross-sectional area A of the wire.
- Decreasing the resistivity of the wire: This will decrease R, thus increasing Im.
- Decreasing the length of the wire: This will also decrease R, thus increasing Im.
- Increasing the cross-sectional area of the wire: This will decrease R, thus increasing Im.
- Increasing the melting point of the wire: This does not affect the resistance directly and is irrelevant to increasing Im.
The only viable options to increase Im are to decrease the resistivity of the wire, decrease the length of the wire, or increase the cross-sectional area of the wire. Among these, the most straightforward method is to decrease the resistivity of the wire.
The value of Im can be increased by decreasing the resistivity of the wire.
Similar Questions
Two identical current carrying coils of radius 10 cm each are placed coaxially0.5 m apart. Find the magnetic fields at the centre of each coil if a current of 0.5 A is passed through each of them in opposite directions. Assume that each coil is made of a single turn.
View SolutionWhat is the effect on the magnetic needle in Oersted's experiment, when (1) a current is passed through the wire (2) the current through the wire is increased (3) The current through the wire to stopped (4) The current through the wire is reversed (5) The distance between jthe magnetic needle and the wire is increased , keeping the current through the wire constant ?
View Solution
Knowledge Check
- Question 1 - Select One
In a bent wire shown in figure, a current I is passed. Find the value of B at the common centre.
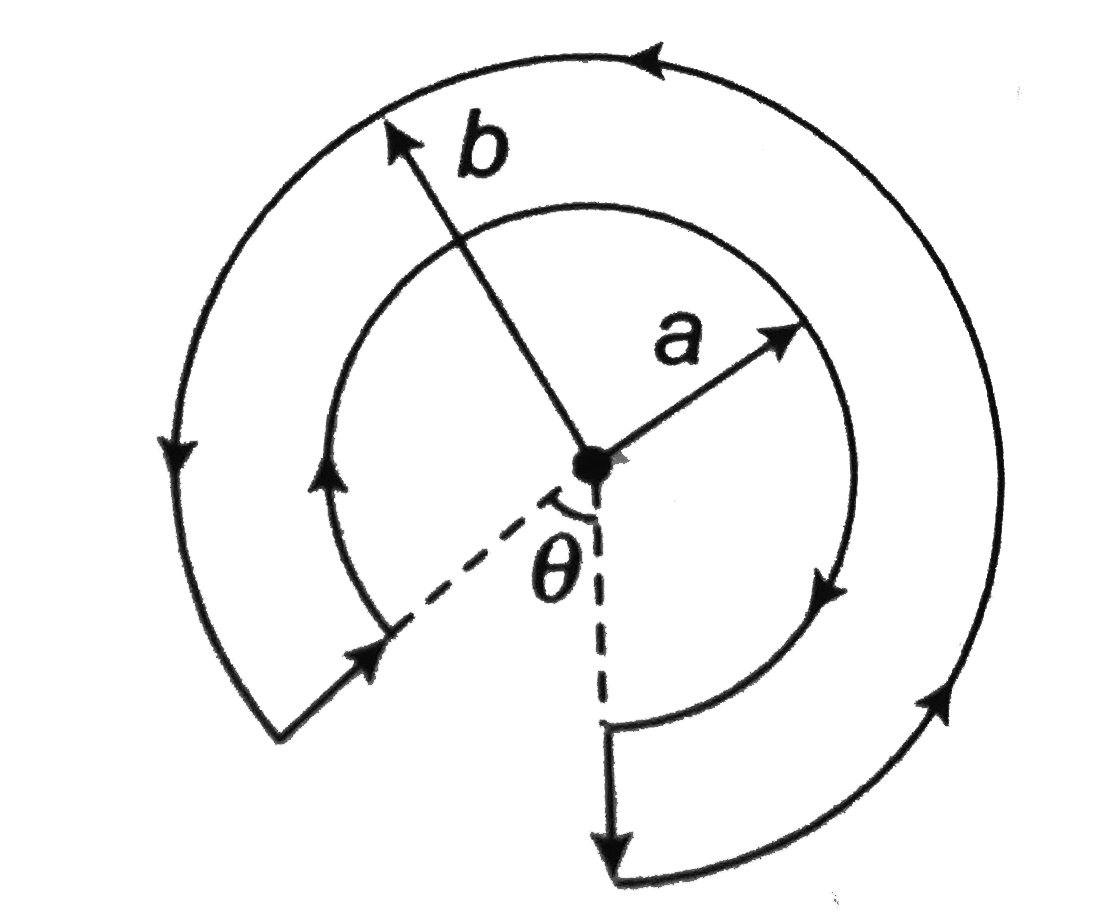 Aμ0I(b−a)(2π−θ)4πabBμ0la(2π−θ)4πbCμ0lb(2π−θ)4πaDμ0labθ4π
Aμ0I(b−a)(2π−θ)4πabBμ0la(2π−θ)4πbCμ0lb(2π−θ)4πaDμ0labθ4π - Question 2 - Select One
A piece of fuse wire melts when a current of15 ampere flows through it. With this current, if it dissipates 22.5 W , the resistance of fuse wire will be
AZeroB10ΩC1ΩD0.10Ω - Question 3 - Select One
If the current I through a resistor is increased by 100% (assume that temperature remains unchanged), the increase in power dissipated will be :
A100%B200%C300%D400%
A long wire is bent as shown in Fig. what will be the magnitude and direction of the field at the centre O of the circular portion, if a current I is passed through the wire ? Assume that the various portions of the wire do not touch at point P.
 View Solution
View SolutionWhen current passes through a conductor then its temperature increases due to heating effect. Which of the following quantities do change due to heating?
View SolutionWhen two terminals of a cell are directly connected to each other, current I passes through it. If 12 such cell are to be connected in such a mannat I is the maximum current then the combination would b
View SolutionA current i passes through a wire of length l , radius of cross-section r and resistivity ρ . The rate of heat generation is
View SolutionIf same current I passing through two parallel wires separated by a distance b, then force per unit length will he
View Solution

