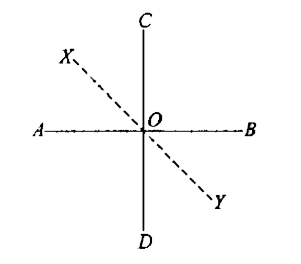
AB and CD are two identical rods each of length l and mass m joined to form a cross. The moment of inertia of these two rods about a bisector (xy) of the angle between the rods is:

A

$\frac{m I^{2}}{6}$

B

$\frac{m I^{2}}{3}$

C

$\frac{m I^{2}}{12}$

D

$\frac{2 m I^{2}}{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Moment of inertia of the combined rods about an axis passing through their point of intersection O and perpendicular to the plane of the rods is
$I_{0} = \frac{m I^{2}}{12} + \frac{m I^{2}}{12} = \frac{m I^{2}}{6}$
Now xy and are two mutually perpendicular axes passing through O lying in the plane of two rods. Then by symmetry.

$I_{X Y} = I_{X' Y'} = I$ (Say)
and $I_{X Y} + I_{X' Y'} = I_{0}$ (from theorem of perpendicular axes).
or $2 I = \frac{m I^{2}}{6}$ So, $I = \frac{m I^{2}}{12}$

|

Updated on:21/07/2023

Class 12 PHYSICS ROTATIONAL MOTION

Similar Questions

Knowledge Check

Question 1 - Select One
AB and CD are two indential rods each of length L and mass M joined to from a cross. Find the M.L of the system about a bisector of the angel between the rods (XY):

A $\frac{M L^{2}}{12}$
B $\frac{M L^{2}}{6}$
C $\frac{M L^{2}}{3}$
D $\frac{4 M L^{2}}{3}$
Question 2 - Select One
Four thin uniform rods each of length L and mass m are joined to form a square . The moment of inertia of square about an axis along its one diagonal is
A $\frac{m L^{2}}{6}$
B $\frac{2}{3} m L^{2}$
C $\frac{3 m L^{2}}{4}$
D $\frac{4 m L^{2}}{3}$
Question 3 - Select One
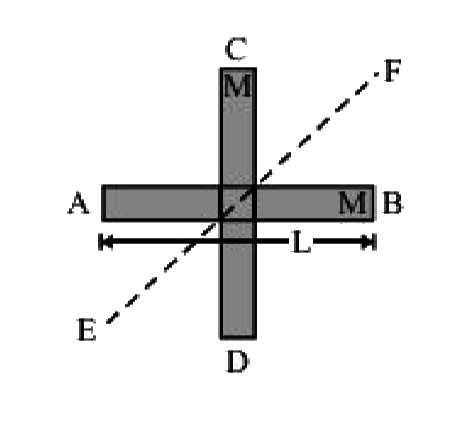
Two uniform thin identical rods AB and CD each of mass M and length L are joined so as to form a cross as shown. The moment of inertia of the cross about a bisector line EF is :-

A $\frac{M L^{2}}{6}$
B $\frac{M L^{2}}{4}$
C $\frac{M L^{2}}{12}$
D $\frac{M L^{2}}{3}$

Recommended Questions

Home
Ask Doubt
Profile